Difference between revisions of "Manuals/calci/HILBERT"
Jump to navigation
Jump to search
| Line 5: | Line 5: | ||
*This function gives matrix of order 3x3 with the property of Hilbert. | *This function gives matrix of order 3x3 with the property of Hilbert. | ||
*A Hilbert matrix, is a square matrix with entries being the unit fractions. i.e.,<math>H_{ij}=\frac{1}{i+j-1}. | *A Hilbert matrix, is a square matrix with entries being the unit fractions. i.e.,<math>H_{ij}=\frac{1}{i+j-1}. | ||
| − | *Example for 5x5 Hilbert matrix is: | + | *Example for 5x5 Hilbert matrix is: <math>\begin{bmatrix} |
1 & \frac{1}{2} & \frac{1}{3} & \frac{1}{4} & \frac{1}{5} \\ | 1 & \frac{1}{2} & \frac{1}{3} & \frac{1}{4} & \frac{1}{5} \\ | ||
\frac{1}{2} & \frac{1}{3} & \frac{1}{4} & \frac{1}{5} & \frac{1}{6} \\ | \frac{1}{2} & \frac{1}{3} & \frac{1}{4} & \frac{1}{5} & \frac{1}{6} \\ | ||
Revision as of 12:42, 24 April 2015
MATRIX("HILBERT",order)
- is the order of the Hilbert matrix.
Description
- This function gives matrix of order 3x3 with the property of Hilbert.
- A Hilbert matrix, is a square matrix with entries being the unit fractions. i.e.,.
- The Hilbert matrix is an example of a Hankel matrix.
- The Hilbert matrix is symmetric and positive definite.
- Also Hilbert matrices are canonical examples of ill-conditioned matrices, making them notoriously difficult to use in numerical computation.
- Here MATRIX("hilbert") gives the hilbert matrices with a decimal places .
- i.e., For 1/2 it will show 0.5, 1/3 will show 0.333 and so on.
 is the order of the Hilbert matrix.
is the order of the Hilbert matrix.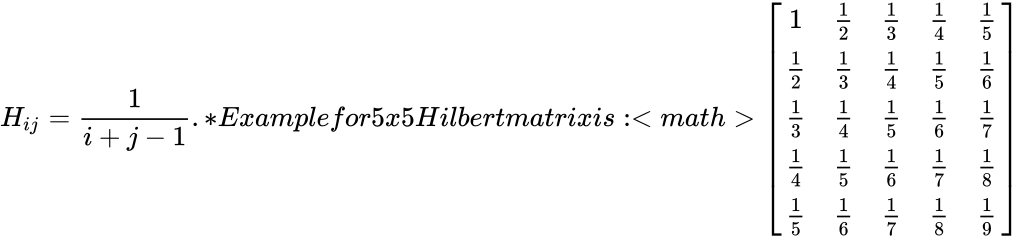 .
.