Difference between revisions of "Manuals/calci/LEVENESTEST"
Jump to navigation
Jump to search
| Line 2: | Line 2: | ||
*<math>xRange</math> is the set of values for the test. | *<math>xRange</math> is the set of values for the test. | ||
*<math>ConfidenceLevel</math> is the value from 0 to 1. | *<math>ConfidenceLevel</math> is the value from 0 to 1. | ||
| − | *<math>LogicalValue</math> is either TRUE or FALSE. | + | *<math>LogicalValue</math> is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube. |
==Description== | ==Description== | ||
| Line 9: | Line 9: | ||
*Equal variances across samples is called homogeneity of variance or homoscedasticity. | *Equal variances across samples is called homogeneity of variance or homoscedasticity. | ||
*To do the Levenes test we need the following assumptions: | *To do the Levenes test we need the following assumptions: | ||
| − | 1.The Samples from the populations are | + | 1.The Samples from the populations are independent of one another. |
2. The population under consideration are Normally Distributed. | 2. The population under consideration are Normally Distributed. | ||
*For three or more variables the following statistical tests for homogeneity of variances are commonly used: | *For three or more variables the following statistical tests for homogeneity of variances are commonly used: | ||
| Line 45: | Line 45: | ||
==Example== | ==Example== | ||
| − | {| class="wikitable" | + | {| class="wikitable"|- |
| − | | | + | | 3067 || 3200 |
|- | |- | ||
| − | + | | 2730 || 2777 | |
|- | |- | ||
| − | + | | 2840 || 2623 | |
| − | | | ||
|- | |- | ||
| − | + | | 2913 || 3044 | |
| − | | | ||
|- | |- | ||
| − | ! | + | | 2789 || 2834 |
| − | | | + | |} |
| − | |- | + | #=LEVENESTEST(B1:C5,.05,0) |
| − | + | ||
| − | | | + | {| class="SpreadSheet notepad' |
| − | |- | + | |+ LEVENES TEST |
| − | + | ||
| − | | | + | |
| − | |- | + | |
| − | + | ! Stats | |
| − | | | + | |
| − | |- | + | ! Data1 |
| − | + | ||
| − | | | + | ! Data2 |
| + | |||
| + | |||
| + | |- | ||
| + | | Median | ||
| + | |||
| + | | 2840 | ||
| + | |||
| + | | 2834 | ||
| + | |||
| + | |||
| + | |- | ||
| + | | Mean | ||
| + | |||
| + | | 2867.8 | ||
| + | |||
| + | | 2895.6 | ||
| + | |||
| + | |||
| + | |- | ||
| + | | Variance | ||
| + | |||
| + | | 16923.7 | ||
| + | |||
| + | | 51713.3 | ||
| + | |||
| + | |||
| + | |- | ||
| + | | Count | ||
| + | |||
| + | | 5 | ||
| + | |||
| + | | 5 | ||
| + | |||
| + | |||
| + | |- | ||
| + | | df | ||
| + | |||
| + | | 4 | ||
| + | |||
| + | | 4 | ||
| + | |||
| + | |} | ||
| + | |||
| + | {| class="SpreadSheet notepad' | ||
| + | |+ Regression Analysis | ||
| + | SUMMARY OUTPUT | ||
| + | |||
| + | |||
| + | ! LevenesTest | ||
| + | |||
| + | ! Statistics | ||
| + | |||
| + | |||
| + | |- | ||
| + | | W | ||
| + | |||
| + | | 1.0439235110342522 | ||
| + | |||
| + | |||
| + | |- | ||
| + | | F-Test | ||
| + | |||
| + | | 0.38245649772919 | ||
| + | |||
| + | |||
| + | |- | ||
| + | | a | ||
| + | |||
| + | | 0.05 | ||
| + | |||
| + | |||
| + | |- | ||
| + | | F | ||
| + | |||
| + | | 0.32726010523405 | ||
| + | |||
| + | |||
| + | |- | ||
| + | | p 1 & 2 Tail | ||
| + | |||
| + | | 0.1524069466470822 | ||
| + | |||
| + | | 0.3048138932941644 | ||
| + | |||
|} | |} | ||
| − | |||
Revision as of 13:28, 29 April 2015
LEVENESTEST(xRange,ConfidenceLevel,NewTableFlag)
- is the set of values for the test.
- is the value from 0 to 1.
- is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.
Description
- This function used to test the Homogeneity of variances.
- Levene's test is used to test the Samples have equal variances.
- Equal variances across samples is called homogeneity of variance or homoscedasticity.
- To do the Levenes test we need the following assumptions:
1.The Samples from the populations are independent of one another. 2. The population under consideration are Normally Distributed.
- For three or more variables the following statistical tests for homogeneity of variances are commonly used:
1.Levene's Test. 2.Bartlett Test.
- Levene's test is an alternative to the Bartlett test.
- If the data surely is of normally distributed or nearly to normally distributed then we can use the Bartlett test.
- The Levene's test is defined as
. =Not all of the variances are equal.
- Normally there are three versions of the Levenes test.
- There are
- 1.Use of Mean.
- 2.Use of Median.
- 3.Use of 10% of Trimmed Mean.
- The Levene test statistic is:
.
- where is the result of the test.
- is the number of different groups to which the sampled cases belong.
- is the total number of cases in all groups.
- is the number of cases in the group.
- case from the group.
- Zij is satisfying the one of the following conditions:
- 1.,Where is the Mean of the subgroup.
- 2.,Where is the Median of the subgroup
- 3.,Where is the 10%Trimmed Mean of the subgroup.
- Levene's Testing Procedure:
- 1. checking the assumptions.
- 2.State the Null(H0) and alternative(H1) hypothesis.
- 3.Decide on the Significance level (α).
- 4.Finding the Critical value and Rejection Region.Here ,.
- 5.Compute the Levenes statistic using the formula.
- 6.Then decision of the value of the test statistic,W is falls in the rejection region or if p-value ≤ α, then reject .Otherwise, fail to reject . For the computation p-value we have to use the value of and .
- 7. Finally we have to conclude that the rejection of or fail to rejection according to the test statistic at the significance level.
Example
| 3067 | 3200 |
| 2730 | 2777 |
| 2840 | 2623 |
| 2913 | 3044 |
| 2789 | 2834 |
- =LEVENESTEST(B1:C5,.05,0)
| Stats | Data1 | Data2
|
|---|---|---|
| Median | 2840 | 2834
|
| Mean | 2867.8 | 2895.6
|
| Variance | 16923.7 | 51713.3
|
| Count | 5 | 5
|
| df | 4 | 4 |
| LevenesTest | Statistics
| |
|---|---|---|
| W | 1.0439235110342522
| |
| F-Test | 0.38245649772919
| |
| a | 0.05
| |
| F | 0.32726010523405
| |
| p 1 & 2 Tail | 0.1524069466470822 | 0.3048138932941644 |
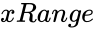 is the set of values for the test.
is the set of values for the test.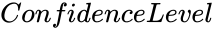 is the value from 0 to 1.
is the value from 0 to 1.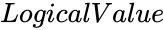 is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.
is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.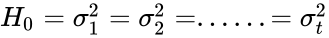 .
.
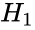 =Not all of the variances are equal.
=Not all of the variances are equal.
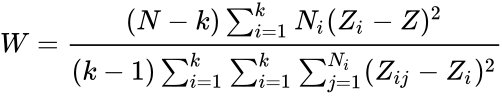 .
.
 is the result of the test.
is the result of the test. is the number of different groups to which the sampled cases belong.
is the number of different groups to which the sampled cases belong.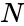 is the total number of cases in all groups.
is the total number of cases in all groups.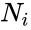 is the number of cases in the
is the number of cases in the 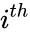 group.
group.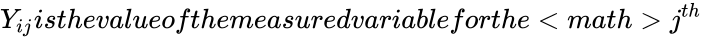 case from the
case from the 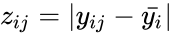 ,Where
,Where 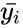 is the Mean of the
is the Mean of the 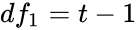 ,
,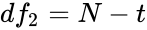 .
.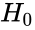 .Otherwise, fail to reject
.Otherwise, fail to reject 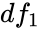 and
and 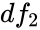 .
.