Difference between revisions of "Manuals/calci/PASCAL"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''PASCAL'''</div><br/>") |
|||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''PASCAL'''</div><br/> | + | <div style="font-size:30px">'''MATRIX("PASCAL",order)'''</div><br/> |
| + | *<math>order</math> is the size of the Pascal matrix. | ||
| + | |||
| + | ==Description== | ||
| + | *This function returns the matrix of any order with the property of Pascal. | ||
| + | *The Pascal matrix is an infinite matrix containing the binomial coefficients as its elements. | ||
| + | *To obtain a pascal matrix there are three ways: as either an upper-triangular matrix(U), a lower-triangular matrix(L), or a symmetric matrix(S). | ||
| + | *Example for these matrices are: | ||
| + | <math>L_4 =\begin{pmatrix} | ||
| + | 54 & 0 & 0 & 0 \\ | ||
| + | 20 & 34 & 0 & 0 \\ | ||
| + | 57 & 89 & -70 & 0 \\ | ||
| + | 71 & -4 & -52 & 72 \\ | ||
| + | \end{pmatrix}</math> | ||
| + | <math>U_4 =\begin{pmatrix} | ||
| + | 64 & 22 & -91 & -86 \\ | ||
| + | 0 & 61 & 62 & -62 \\ | ||
| + | 0 & 0 & 30 & -81 \\ | ||
| + | 0 & 0 & 0 & -61 \\ | ||
| + | \end{pmatrix}</math> | ||
| + | <math>S_4 =\begin{pmatrix} | ||
| + | 41 & 74 & 15 & -47 \\ | ||
| + | 74 & -16 & 37 & 97 \\ | ||
| + | 15 & 37 & 24 & -88 \\ | ||
| + | -47 & 97 & -88 & -69 \\ | ||
| + | \end{pmatrix}</math> | ||
| + | *The amazing relationship of these matrices are:<math>S_n = L_nU_n</math>. | ||
| + | *And its determinants also 1.i.e.,<math> |S_n|=|L_n|=|U_n|=1 </math> | ||
| + | *The Pascal matrix can actually be constructed by taking the matrix exponential of a special subdiagonal or superdiagonal matrix. | ||
| + | *The elements of the symmetric Pascal matrix are the binomial coefficients, i.e. | ||
| + | <math>S_{ij} = {n \choose r} = \frac{n!}{r!(n-r)!},</math>, where n=i+j, r=i. | ||
| + | *In other words, | ||
| + | <math>S_{ij} = _{i+j}{C}_{i} = \frac{(i+j)!}{(i)!(j)!}</math>. | ||
| + | *Here MATRIX("pascal") is showing the pascal matrix of order 3. | ||
| + | *So users can change the order of the matrix also. | ||
Revision as of 12:30, 30 April 2015
MATRIX("PASCAL",order)
- is the size of the Pascal matrix.
Description
- This function returns the matrix of any order with the property of Pascal.
- The Pascal matrix is an infinite matrix containing the binomial coefficients as its elements.
- To obtain a pascal matrix there are three ways: as either an upper-triangular matrix(U), a lower-triangular matrix(L), or a symmetric matrix(S).
- Example for these matrices are:
- The amazing relationship of these matrices are:.
- And its determinants also 1.i.e.,
- The Pascal matrix can actually be constructed by taking the matrix exponential of a special subdiagonal or superdiagonal matrix.
- The elements of the symmetric Pascal matrix are the binomial coefficients, i.e.
, where n=i+j, r=i.
- In other words,
.
- Here MATRIX("pascal") is showing the pascal matrix of order 3.
- So users can change the order of the matrix also.
 is the size of the Pascal matrix.
is the size of the Pascal matrix.

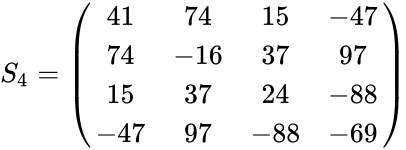
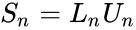 .
.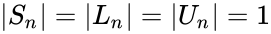
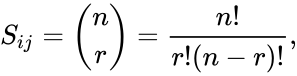 , where n=i+j, r=i.
, where n=i+j, r=i.
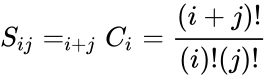 .
.