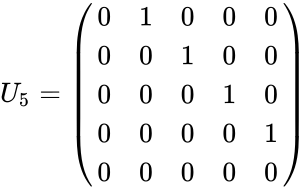Difference between revisions of "Manuals/calci/SHIFT"
Jump to navigation
Jump to search
| Line 19: | Line 19: | ||
0 & 0 & 0 & 0 & 1 \\ | 0 & 0 & 0 & 0 & 1 \\ | ||
0 & 0 & 0 & 0 & 0 | 0 & 0 & 0 & 0 & 0 | ||
| − | \end{pmatrix} | + | \end{pmatrix}</math> |
<math>L_5 = \begin{pmatrix} | <math>L_5 = \begin{pmatrix} | ||
0 & 0 & 0 & 0 & 0 \\ | 0 & 0 & 0 & 0 & 0 \\ | ||
| Line 26: | Line 26: | ||
0 & 0 & 1 & 0 & 0 \\ | 0 & 0 & 1 & 0 & 0 \\ | ||
0 & 0 & 0 & 0 & 0 | 0 & 0 & 0 & 0 & 0 | ||
| − | \end{pmatrix} | + | \end{pmatrix}</math> |
*All shift matrices are nilpotent; an n by n shift matrix S becomes the null matrix when raised to the power of its dimension n. | *All shift matrices are nilpotent; an n by n shift matrix S becomes the null matrix when raised to the power of its dimension n. | ||
Revision as of 11:21, 4 May 2015
MATRIX("SHIFT",order)
- is the size of the Shift matrix.
Description
- This function returns shift matrix of order 3.
- A shift matrix is a binary matrix with ones only on the superdiagonal or subdiagonal, and zeroes elsewhere.
- A shift matrix U with ones on the superdiagonal is an upper shift matrix.
- The alternative subdiagonal matrix L is unsurprisingly known as a lower shift matrix.
- Let Z is a shift matrix , then are equal to the matrix A shifted one position down, up left, right, and down along the main diagonal respectively.
- The alternative subdiagonal matrix L is unsurprisingly known as a lower shift matrix.
- The component of U and L are:
.
where is the Kronecker delta symbol.
- For example, the 5×5 shift matrices are:
- All shift matrices are nilpotent; an n by n shift matrix S becomes the null matrix when raised to the power of its dimension n.
 is the size of the Shift matrix.
is the size of the Shift matrix.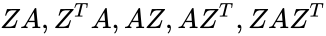 are equal to the matrix A shifted one position down, up left, right, and down along the main diagonal respectively.
are equal to the matrix A shifted one position down, up left, right, and down along the main diagonal respectively. component of U and L are:
component of U and L are: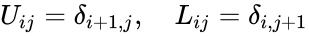 .
.
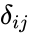 is the Kronecker delta symbol.
is the Kronecker delta symbol.