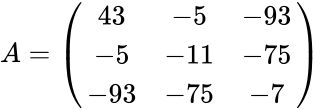Difference between revisions of "Manuals/calci/SYMMETRIC"
Jump to navigation
Jump to search
| Line 4: | Line 4: | ||
==Description== | ==Description== | ||
*This function returns the symmetric matrix of order 3. | *This function returns the symmetric matrix of order 3. | ||
| − | *A symmetric matrix is a square matrix that satisfies <math>A^ | + | *A symmetric matrix is a square matrix that satisfies <math>A^T=A</math>,where <math>A^T</math> denotes the transpose. |
*i.e., A square matrix which is equal to its transpose is called symmetric matrix. | *i.e., A square matrix which is equal to its transpose is called symmetric matrix. | ||
| − | *So <math>a_ | + | *So <math>a_{ij}=a_{ji}</math>. |
| − | *This also implies <math>A^ | + | *This also implies <math>A^{-1}A^T=I</math>, where I is the identity matrix. |
*Because equal matrices have equal dimensions, only square matrices can be symmetric. | *Because equal matrices have equal dimensions, only square matrices can be symmetric. | ||
*An example for the symmetric matrix is | *An example for the symmetric matrix is | ||
| Line 14: | Line 14: | ||
-5 & -11 & -75 \\ | -5 & -11 & -75 \\ | ||
-93 & -75 & -7 \\ | -93 & -75 & -7 \\ | ||
| − | \end{pmatrix} | + | \end{pmatrix} </math> |
*The properties of symmetric matrices are: | *The properties of symmetric matrices are: | ||
*1.Every square diagonal matrix is symmetric, since all off-diagonal entries are zero. | *1.Every square diagonal matrix is symmetric, since all off-diagonal entries are zero. | ||
Revision as of 12:58, 4 May 2015
MATRIX("SYMMETRIC",order)
- is the size of the Symmetric matrix.
Description
- This function returns the symmetric matrix of order 3.
- A symmetric matrix is a square matrix that satisfies ,where denotes the transpose.
- i.e., A square matrix which is equal to its transpose is called symmetric matrix.
- So .
- This also implies , where I is the identity matrix.
- Because equal matrices have equal dimensions, only square matrices can be symmetric.
- An example for the symmetric matrix is
- The properties of symmetric matrices are:
- 1.Every square diagonal matrix is symmetric, since all off-diagonal entries are zero.
- 2.Similarly, each diagonal element of a skew-symmetric matrix must be zero, since each is its own negative.
- 3.Hermitian matrices are a useful generalization of symmetric matrices for complex matrices.
- In Calci, MATRIX("symmetric") gives the symmetric matrix with the integer numbers.
- The other way to give the syntax is MATRIX("symmetric:integer).The syntax is to get the positive numbers symmetric matrix is MATRIX("symmetric:positive integer").
- To get a negative numbers symmetric matrix is MATRIX("symmetric:negative integer").
- Also to get the symmetric matrix with the elements 0 and 1(boolean numbers) users give syntax as MATRIX("symmetric:boolean").
- So using Calci users can get a different types of symmetric matrices.
 is the size of the Symmetric matrix.
is the size of the Symmetric matrix.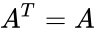 ,where
,where 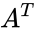 denotes the transpose.
denotes the transpose.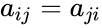 .
.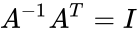 , where I is the identity matrix.
, where I is the identity matrix.