Difference between revisions of "Manuals/calci/PENTADIAGONAL"
Jump to navigation
Jump to search
| Line 13: | Line 13: | ||
0 & a_2 & \cdots & \ddots & \ddots & e_{n-3} & 0 \\ | 0 & a_2 & \cdots & \ddots & \ddots & e_{n-3} & 0 \\ | ||
\vdots & \ddots & \ddots & \ddots & \ddots & d_{n-2} & e_{n-2} \\ | \vdots & \ddots & \ddots & \ddots & \ddots & d_{n-2} & e_{n-2} \\ | ||
| − | \vdots & & \ddots & a_{n-3} & b_{n-2} & c_{n-1} & d_{n-1} \\ | + | \vdots &\cdots& \ddots & a_{n-3} & b_{n-2} & c_{n-1} & d_{n-1} \\ |
0 & \cdots & \cdots & 0 & a_{n-2} & b_{n-1} & c_n | 0 & \cdots & \cdots & 0 & a_{n-2} & b_{n-1} & c_n | ||
\end{pmatrix}</math>. | \end{pmatrix}</math>. | ||
Revision as of 12:34, 5 May 2015
MATRIX("PENTADIAGONAL",order)
- is the size of the Pentadiagonal matrix.
Description
- This function gives the pentadiagonal matrix of order 3.
- A pentadiagonal matrix is a matrix that is nearly diagonal.
- So it is a matrix in which the only nonzero entries are on the main diagonal, and the first two diagonals above and below it.
- The form of pentadiagonal matrix is:
.
- When n is the size of the matrix, a pentadiagonal matrix has atmost 5n-6 nonzero entries.
- Here MATIRX("pentadiagonal") is showing the penta diagonal matrix of order 3 with the integer numbers.
- Also in Calci users can get a deimal values with positive and negative numbers.
- The syntax is to get the decimal penta diagonal matrix is MATRIX("pentadiagonal:negative") and MATRIX(pentadiagonal:positive")
 is the size of the Pentadiagonal matrix.
is the size of the Pentadiagonal matrix.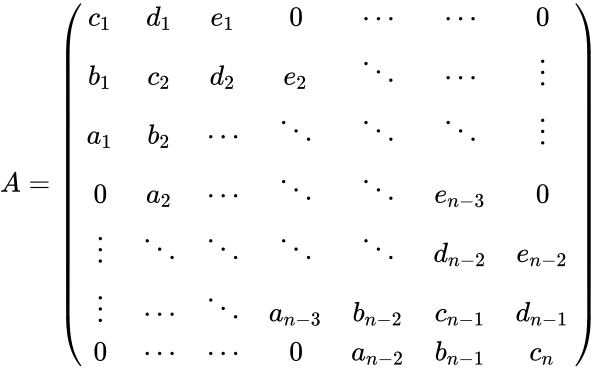 .
.