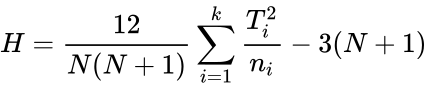Difference between revisions of "Manuals/calci/KRUSKALWALLISTEST"
Jump to navigation
Jump to search
| Line 186: | Line 186: | ||
| style="width: 173px;" | 0.05 | | style="width: 173px;" | 0.05 | ||
|} | |} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/LEVENESTEST| LEVENESTEST]] | ||
| + | *[[Manuals/calci/MOODSMEDIANTEST| MOODSMEDIANTEST]] | ||
| + | *[[Manuals/calci/RIEMANNZETA| RIEMANNZETA]] | ||
| + | |||
==References== | ==References== | ||
Revision as of 10:01, 12 May 2015
KRUSKALWALLISTEST(Array,Confidencelevel,Logicalvalue)
- is the set of values to find the test statistic.
- is the value between 0 and 1.
- is either TRUE or FALSE.
Description
- This function gives the test statistic value of the Kruskal Wallis test.
- It is one type of Non parametric test.
- It is a logical extension of the Wilcoxon-Mann-Whitney Test.
- The parametric equivalent of the Kruskal-Wallis test is the one-way analysis of variance (ANOVA).
- This test is used for comparing more than two sample that are independent or not related.
- It is used to test the null hypothesis that all populations have identical distribution functions against the alternative hypothesis that at least two of the samples differ only with respect to Median.
- Kruskal–Wallis is also used when the examined groups are of unequal size.
- When the Kruskal-Wallis test leads to significant results, then at least one of the samples is different from the other samples.
- The test does not identify where the differences occur or how many differences actually occur.
- Since it is a non-parametric method, the Kruskal–Wallis test does not assume a normal distribution of the residuals, unlike the analogous one-way analysis of variance.
- However, the test does assume an identically shaped and scaled distribution for each group, except for any difference in medians.
- The Kruskal Wallis test data are having the following properties:
- 1.The data points must be independent from each other.
- 2.The distributions do not have to be normal and the variances do not have to be equal.
- 3.The data points must be more than five per sample.
- 4.All individuals must be selected at random from the population.
- 5.All individuals must have equal chance of being selected.
- 6.Sample sizes should be as equal as possible but some differences are allowed.
- Steps for Kruskal Wallis Test:
- 1. Define Null and Alternative Hypotheses:
- Null Hypotheses:There is no difference between the conditions.
- Alternative Hypotheses:There is a difference between the conditions.
- 2.State Alpha:Alpha=0.05.
- 3.Calculate degrees of freedom:df = k – 1, where k = number of groups.
- 4.State Decision Rule:From the Chi squared table calculate the critical value.
- Suppose the is greater than the critical value then reject the null hypothesis
- 5.Calculate the Test Statistic:
- 6.State Results:In this step we have to take a decision of null hypothesis either accept or reject depending on the critical value table.
- 7.State Conclusion:To be significant, our obtained H has to be equal to or LESS than this critical value.
Example
| Method1 | Method2 | Method3 |
| 94 | 82 | 89 |
| 87 | 85 | 68 |
| 90 | 79 | 72 |
| 74 | 84 | 76 |
| 86 | 61 | 69 |
| 97 | 72 | 65 |
| 0 | 80 | 0 |
- =LEVENESTEST(B1:C5,.05,0)
| Method1 | Method2 | Method3 |
| 18 | 11 | 16 |
| 15 | 13 | 3 |
| 17 | 9 | 5.5 |
| 7 | 12 | 8 |
| 14 | 1 | 4 |
| 19 | 5.5 | 2 |
| 10 |
| Method1 | Method2 | Method3 | |
| Sum of Ranks | 90 | 61.5 | 38.5 |
| Group Size | 6 | 7 | 6 |
| R^2/n | 1350 | 540.3214285714286 | 247.04166666666666 |
| TotalRankSum | 190 | ||
| Total Group Size | 19 | ||
| Total R^2/n | 2137.363095238095 | ||
| H | 7.495676691729315 | ||
| df | 2 | ||
| p-value | 0.023568638074462633 | ||
| a | 0.05 |
See Also
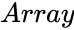 is the set of values to find the test statistic.
is the set of values to find the test statistic.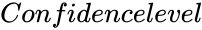 is the value between 0 and 1.
is the value between 0 and 1.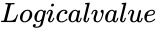 is either TRUE or FALSE.
is either TRUE or FALSE. is greater than the critical value then reject the null hypothesis
is greater than the critical value then reject the null hypothesis