Difference between revisions of "Manuals/calci/ERF"
Jump to navigation
Jump to search
| Line 28: | Line 28: | ||
#ERF(5)=1 | #ERF(5)=1 | ||
#ERF(-3)=NAN | #ERF(-3)=NAN | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|IIuXF5QRBTY|280|center|Gaussian Distribution}} | ||
==See Also== | ==See Also== | ||
Revision as of 14:24, 18 July 2015
ERF(a,b,accuracy)
- is the lower limit and is the upper limit.
- gives accurate value of the solution
Description
- This function gives the value of the error function .
- Error function is the special function which is encountered in integrating the normal distribution.
- In , is the lower limit of the integrating function and is the upper limit of the integrating function.
- Also is optional. When we are omitting the value, then the integral of the error function between 0 and the given value is returned otherwise it will consider the given and values.
- This function is also called Gauss error function.
- is defined by:
- .
- In this case is the lower limit and is the upper limit.
- This function will return the result as error when
1.any one of the argument is non-numeric. 2. or is negative.
ZOS
- The syntax is to calculate error function in ZOS is .
- is the lower limit and is the upper limit.
- gives accurate value of the solution.
- For e.g.,erf(2,3),erf(2,3,0.001)
Examples
- ERF(1,2)=0.15262153
- ERF(3,2)=-0.004655645
- ERF(0,1)=0.842700735
- ERF(5)=1
- ERF(-3)=NAN
 is the lower limit and
is the lower limit and 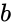 is the upper limit.
is the upper limit.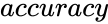 gives accurate value of the solution
gives accurate value of the solution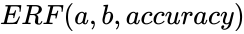 ,
,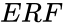 is defined by:
is defined by: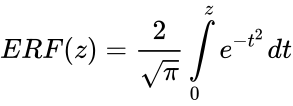
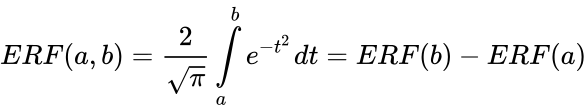 .
.