Difference between revisions of "Manuals/calci/PI"
Jump to navigation
Jump to search
(Created page with "<div id="16SpaceContent" align="left"><div class="ZEditBox" align="justify"> Syntax </div></div> ---- <div id="2SpaceContent" align="left"><div class="ZEditBox" align=...") |
|||
| (8 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''PI()'''</div><br/> |
| − | + | ==Description== | |
| + | *This function gives the value of <math>pi</math>. | ||
| + | *The <math>pi</math> is a mathematical constant with a value approximate to 3.14159. | ||
| + | *It is denoted by the Greek letter <math>\Pi</math>. | ||
| + | *<math>\Pi</math> is commonly defined as the ratio of a circle's circumference <math>C</math> to its diameter <math>d</math>. | ||
| + | *So <math>\Pi =\frac {C}{d}</math>, the ratio <math> \frac {C}{d}</math> is constant, and it is not considering the circle's size. | ||
| + | *<math>\Pi</math> is a transcendental number and irrational number. | ||
| + | *Being an irrational number, <math>\Pi</math> cannot be expressed exactly as a ratio of any two integers . | ||
| + | *But we can express as the fraction <math>\frac {22}{7}</math> is approximate to the <math>\Pi</math> value , also no fraction can be its exact value. | ||
| − | + | ==Examples== | |
| − | + | #=PI() = 3.141592653589793 | |
| − | + | #=PI()/4 = 0.785398163 | |
| + | #=PI()/180 = 0.017453293 | ||
| + | #=PI()/(22/7) = 0.999597663 | ||
| + | #=PI()*(5^2) = 78.53981634(Area of circle with r=5) | ||
| + | #=2*PI()*5 = 31.41592654(Circumference of a circle with r=5). | ||
| − | + | ==Related Videos== | |
| − | + | {{#ev:youtube|jyLRpr2P0MQ|280|center|PI}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==See Also== | |
| + | *[[Manuals/calci/SIN | SIN ]] | ||
| + | *[[Manuals/calci/COS | COS ]] | ||
| + | *[[Manuals/calci/TAN | TAN ]] | ||
| − | + | ==References== | |
| − | + | [http://en.wikipedia.org/wiki/Pi Pi] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 10:26, 10 October 2015
PI()
Description
- This function gives the value of .
- The is a mathematical constant with a value approximate to 3.14159.
- It is denoted by the Greek letter .
- is commonly defined as the ratio of a circle's circumference to its diameter .
- So , the ratio is constant, and it is not considering the circle's size.
- is a transcendental number and irrational number.
- Being an irrational number, cannot be expressed exactly as a ratio of any two integers .
- But we can express as the fraction is approximate to the value , also no fraction can be its exact value.
Examples
- =PI() = 3.141592653589793
- =PI()/4 = 0.785398163
- =PI()/180 = 0.017453293
- =PI()/(22/7) = 0.999597663
- =PI()*(5^2) = 78.53981634(Area of circle with r=5)
- =2*PI()*5 = 31.41592654(Circumference of a circle with r=5).
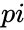 .
.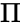 .
. to its diameter
to its diameter  .
.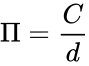 , the ratio
, the ratio  is constant, and it is not considering the circle's size.
is constant, and it is not considering the circle's size.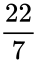 is approximate to the
is approximate to the