Difference between revisions of "Manuals/calci/BIDIAGONAL"
Jump to navigation
Jump to search
| (3 intermediate revisions by 2 users not shown) | |||
| Line 26: | Line 26: | ||
==Examples== | ==Examples== | ||
| − | *1.MATRIX("bidiagonal") | + | *1.MATRIX("bidiagonal") = 70 |
| + | *2.MATRIX("bidiagonal",3) | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Line 35: | Line 36: | ||
| 0 || 0 || 97 | | 0 || 0 || 97 | ||
|} | |} | ||
| − | * | + | *3.MATRIX("bidiagonal",5) |
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Line 48: | Line 49: | ||
| 0 || 0 || 0 || 0 || 87 | | 0 || 0 || 0 || 0 || 87 | ||
|} | |} | ||
| − | * | + | *4.MATRIX("upper-bidiagonal",3) |
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Line 57: | Line 58: | ||
| 0 || 0 || 19 | | 0 || 0 || 19 | ||
|} | |} | ||
| − | * | + | *5.MATRIX("lowerbidiagonal",4) |
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Line 68: | Line 69: | ||
| 0 || 0 || 94 || -33 | | 0 || 0 || 94 || -33 | ||
|} | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|F9wVeCg03rA|280|center|Banded Matrix, Tri-diagonal Matrix}} | ||
==See Also== | ==See Also== | ||
| Line 75: | Line 80: | ||
==References== | ==References== | ||
| + | *[http://en.wikipedia.org/wiki/Bidiagonal_matrix Bidiagonal] | ||
Latest revision as of 00:27, 26 October 2015
MATRIX("BIDIAGONAL",order)
- is the size of the Bidiagonal matrix.
Description
- This function returns the matrix with the property of bidiagonal.
- A bidiagonal matrix has non zero entries only on the main bidiagonal and either the first super-diagonal and first sub-diagonal.
- In Calci,users will get different types of bidiagonal matrices.
- There are two types are there lower bidiagonal and upper bidiagonal.
- When the diagonal below the main diagonal has the non-zero entries the matrix is lower bidiagonal.
- When the diagonal above the main diagonal has the non-zero entries the matrix is upper bidiagonal.
- The example of lower bidiagonal matrix is:
- The example of a upper bidiagonal matrix is:
- The syntax of lower and upper bidiagonal matrices are MATRIX("lowerbidiagonal") or MATRIX("lower-bidiagonal") and MATRIX("upperbidiagonal") or MATRIX("upper-bidiagonal")
Examples
- 1.MATRIX("bidiagonal") = 70
- 2.MATRIX("bidiagonal",3)
| -63 | 97 | 0 |
| 0 | 44 | 65 |
| 0 | 0 | 97 |
- 3.MATRIX("bidiagonal",5)
| 77 | -7 | 0 | 0 | 0 |
| 0 | 83 | 56 | 0 | 0 |
| 0 | 0 | 2 | -88 | 0 |
| 0 | 0 | 0 | -88 | -59 |
| 0 | 0 | 0 | 0 | 87 |
- 4.MATRIX("upper-bidiagonal",3)
| -5 | 40 | 0 |
| 0 | 5 | 71 |
| 0 | 0 | 19 |
- 5.MATRIX("lowerbidiagonal",4)
| 87 | 0 | 0 | 0 |
| 8 | -13 | 0 | 0 |
| 0 | -70 | 82 | 0 |
| 0 | 0 | 94 | -33 |
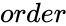 is the size of the Bidiagonal matrix.
is the size of the Bidiagonal matrix.
