Difference between revisions of "Manuals/calci/MATRIXOPERATORS"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''MATRIX OPERATORS'''</div><br/>") |
|||
| (6 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''MATRIX OPERATORS'''</div><br/> | + | <div style="font-size:30px">'''MATRIX OPERATORS("op-type")'''</div><br/> |
| + | *<math>op-type</math> is the value of the function. | ||
| + | |||
| + | ==Description== | ||
| + | *This function gives the matrix with the values of 0 and 1. | ||
| + | *Here MATRIX("op-type"), where op-type is the type of operations. | ||
| + | *There are 5 types of operations:1. Logical 2. Boolean 3. Relation 4. Binary 5.(0,1). | ||
| + | *A logical matrix, binary matrix, relation matrix, Boolean matrix, or (0,1) matrix is a matrix with entries from the Boolean domain B = {0, 1}. | ||
| + | *Such a matrix can be used to represent a binary relation between a pair of finite sets. | ||
| + | *These types of matrices having only with the elements 0 and 1. | ||
| + | *The syntax of matrices are Logical: MATRIX("logical") gives the matrix with the element 0 and 1 of order 3x3. | ||
| + | *Boolean:MATRIX("boolean") or MATRIX("boolean",5). | ||
| + | *Relation:MATRIX("relation") | ||
| + | *Binary:MATRIX("binary",5) is showing the matrix of order 5x5 with 0 and 1. | ||
| + | *(0,1): MATRIX("(0,1)") is showing the matrix of element 0 and 1. | ||
| + | |||
| + | ==Examples== | ||
| + | *MATRIX("logical") = 1 | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 0 || 0 || 1 | ||
| + | |- | ||
| + | | 1 || 0 || 1 | ||
| + | |- | ||
| + | | 0 || 1 || 1 | ||
| + | |} | ||
| + | |||
| + | *MATRIX("binary",4) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 1 || 1 || 1 || 0 | ||
| + | |- | ||
| + | | 0 || 0 || 0 || 0 | ||
| + | |- | ||
| + | | 1 || 0 || 0 || 0 | ||
| + | |- | ||
| + | | 1 || 1 || 1 || 0 | ||
| + | |} | ||
| + | *MATRIX("boolean",2) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 1 || 0 | ||
| + | |- | ||
| + | | 0 || 1 | ||
| + | |} | ||
| + | *MATRIX("relation",3) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 1 || 1 || 1 | ||
| + | |- | ||
| + | | 0 || 0 || 0 | ||
| + | |- | ||
| + | | 0 || 0 || 0 | ||
| + | |} | ||
| + | |||
| + | *MATRIX("(0,1)",5) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 0 || 1 || 1 || 1 || 0 | ||
| + | |- | ||
| + | | 1 || 0 || 1 || 1 || 1 | ||
| + | |- | ||
| + | | 0 || 0 || 0 || 1 || 1 | ||
| + | |- | ||
| + | | 0 || 1 || 1 || 0 || 0 | ||
| + | |- | ||
| + | | 1 || 1 || 0 || 1 || 1 | ||
| + | |} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/ARROWHEAD| ARROWHEAD]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://en.wikipedia.org/wiki/Logical_matrix Logical Matrix] | ||
| + | *[http://mathworld.wolfram.com/01-Matrix.html (0,1) Matrix] | ||
Latest revision as of 01:24, 26 October 2015
MATRIX OPERATORS("op-type")
- is the value of the function.
Description
- This function gives the matrix with the values of 0 and 1.
- Here MATRIX("op-type"), where op-type is the type of operations.
- There are 5 types of operations:1. Logical 2. Boolean 3. Relation 4. Binary 5.(0,1).
- A logical matrix, binary matrix, relation matrix, Boolean matrix, or (0,1) matrix is a matrix with entries from the Boolean domain B = {0, 1}.
- Such a matrix can be used to represent a binary relation between a pair of finite sets.
- These types of matrices having only with the elements 0 and 1.
- The syntax of matrices are Logical: MATRIX("logical") gives the matrix with the element 0 and 1 of order 3x3.
- Boolean:MATRIX("boolean") or MATRIX("boolean",5).
- Relation:MATRIX("relation")
- Binary:MATRIX("binary",5) is showing the matrix of order 5x5 with 0 and 1.
- (0,1): MATRIX("(0,1)") is showing the matrix of element 0 and 1.
Examples
- MATRIX("logical") = 1
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
- MATRIX("binary",4)
| 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 |
- MATRIX("boolean",2)
| 1 | 0 |
| 0 | 1 |
- MATRIX("relation",3)
| 1 | 1 | 1 |
| 0 | 0 | 0 |
| 0 | 0 | 0 |
- MATRIX("(0,1)",5)
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
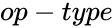 is the value of the function.
is the value of the function.