Difference between revisions of "Manuals/calci/PASCAL"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''PASCAL'''</div><br/>") |
|||
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''PASCAL'''</div><br/> | + | <div style="font-size:30px">'''MATRIX("PASCAL",order)'''</div><br/> |
| + | *<math>order</math> is the size of the Pascal matrix. | ||
| + | |||
| + | ==Description== | ||
| + | *This function returns the matrix of any order with the property of Pascal. | ||
| + | *The Pascal matrix is an infinite matrix containing the binomial coefficients as its elements. | ||
| + | *To obtain a pascal matrix there are three ways: as either an upper-triangular matrix(U), a lower-triangular matrix(L), or a symmetric matrix(S). | ||
| + | *Example for these matrices are | ||
| + | <math>L_4 =\begin{pmatrix} | ||
| + | 54 & 0 & 0 & 0 \\ | ||
| + | 20 & 34 & 0 & 0 \\ | ||
| + | 57 & 89 & -70 & 0 \\ | ||
| + | 71 & -4 & -52 & 72 \\ | ||
| + | \end{pmatrix}</math> | ||
| + | <math>U_4 =\begin{pmatrix} | ||
| + | 64 & 22 & -91 & -86 \\ | ||
| + | 0 & 61 & 62 & -62 \\ | ||
| + | 0 & 0 & 30 & -81 \\ | ||
| + | 0 & 0 & 0 & -61 \\ | ||
| + | \end{pmatrix}</math> | ||
| + | <math>S_4 =\begin{pmatrix} | ||
| + | 41 & 74 & 15 & -47 \\ | ||
| + | 74 & -16 & 37 & 97 \\ | ||
| + | 15 & 37 & 24 & -88 \\ | ||
| + | -47 & 97 & -88 & -69 \\ | ||
| + | \end{pmatrix}</math> | ||
| + | *The amazing relationship of these matrices are:<math>S_n = L_nU_n</math>. | ||
| + | *And its determinants also 1.i.e.,<math> |S_n|=|L_n|=|U_n|=1 </math> | ||
| + | *The Pascal matrix can actually be constructed by taking the matrix exponential of a special subdiagonal or superdiagonal matrix. | ||
| + | *The elements of the symmetric Pascal matrix are the binomial coefficients, i.e. | ||
| + | <math>S_{ij} = {n \choose r} = \frac{n!}{r!(n-r)!},</math>, where n=i+j, r=i. | ||
| + | *In other words, | ||
| + | <math>S_{ij} = _{i+j}{C}_{i} = \frac{(i+j)!}{(i)!(j)!}</math>. | ||
| + | *Here MATRIX("pascal") is showing the pascal matrix of order 3. | ||
| + | *So users can change the order of the matrix also. | ||
| + | |||
| + | ==Examples== | ||
| + | *1.MATRIX("pascal") =1 | ||
| + | *2.MATRIX("pascal",3) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 1 || 1 || 1 | ||
| + | |- | ||
| + | | 1 || 2 || 3 | ||
| + | |- | ||
| + | | 1 || 3 || 6 | ||
| + | |} | ||
| + | *3.MATRIX("pascal",5) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 1 || 1 || 1 || 1 || 1 | ||
| + | |- | ||
| + | | 1 || 2 || 3 || 4 || 5 | ||
| + | |- | ||
| + | | 1 || 3 || 6 || 10 || 15 | ||
| + | |- | ||
| + | | 1 || 4 || 10 || 20 || 35 | ||
| + | |- | ||
| + | | 1 || 5 || 15 || 35 || 70 | ||
| + | |} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/ANTIDIAGONAL| ANTIDIAGONAL]] | ||
| + | *[[Manuals/calci/CONFERENCE| CONFERENCE]] | ||
| + | *[[Manuals/calci/TRIANGULAR| TRIANGULAR]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://en.wikipedia.org/wiki/Pascal_matrix Pascal Matrix] | ||
Latest revision as of 01:32, 26 October 2015
MATRIX("PASCAL",order)
- is the size of the Pascal matrix.
Description
- This function returns the matrix of any order with the property of Pascal.
- The Pascal matrix is an infinite matrix containing the binomial coefficients as its elements.
- To obtain a pascal matrix there are three ways: as either an upper-triangular matrix(U), a lower-triangular matrix(L), or a symmetric matrix(S).
- Example for these matrices are
- The amazing relationship of these matrices are:.
- And its determinants also 1.i.e.,
- The Pascal matrix can actually be constructed by taking the matrix exponential of a special subdiagonal or superdiagonal matrix.
- The elements of the symmetric Pascal matrix are the binomial coefficients, i.e.
, where n=i+j, r=i.
- In other words,
.
- Here MATRIX("pascal") is showing the pascal matrix of order 3.
- So users can change the order of the matrix also.
Examples
- 1.MATRIX("pascal") =1
- 2.MATRIX("pascal",3)
| 1 | 1 | 1 |
| 1 | 2 | 3 |
| 1 | 3 | 6 |
- 3.MATRIX("pascal",5)
| 1 | 1 | 1 | 1 | 1 |
| 1 | 2 | 3 | 4 | 5 |
| 1 | 3 | 6 | 10 | 15 |
| 1 | 4 | 10 | 20 | 35 |
| 1 | 5 | 15 | 35 | 70 |
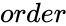 is the size of the Pascal matrix.
is the size of the Pascal matrix.

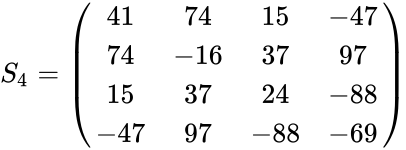
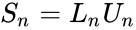 .
.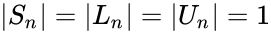
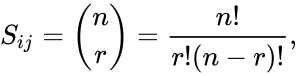 , where n=i+j, r=i.
, where n=i+j, r=i.
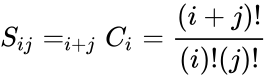 .
.