Difference between revisions of "Manuals/calci/PASCAL"
Jump to navigation
Jump to search
| Line 36: | Line 36: | ||
==Examples== | ==Examples== | ||
| − | *1.MATRIX("pascal") | + | *1.MATRIX("pascal") =1 |
| + | *2.MATRIX("pascal",3) | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Line 45: | Line 46: | ||
| 1 || 3 || 6 | | 1 || 3 || 6 | ||
|} | |} | ||
| − | * | + | *3.MATRIX("pascal",5) |
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
Latest revision as of 01:32, 26 October 2015
MATRIX("PASCAL",order)
- is the size of the Pascal matrix.
Description
- This function returns the matrix of any order with the property of Pascal.
- The Pascal matrix is an infinite matrix containing the binomial coefficients as its elements.
- To obtain a pascal matrix there are three ways: as either an upper-triangular matrix(U), a lower-triangular matrix(L), or a symmetric matrix(S).
- Example for these matrices are
- The amazing relationship of these matrices are:.
- And its determinants also 1.i.e.,
- The Pascal matrix can actually be constructed by taking the matrix exponential of a special subdiagonal or superdiagonal matrix.
- The elements of the symmetric Pascal matrix are the binomial coefficients, i.e.
, where n=i+j, r=i.
- In other words,
.
- Here MATRIX("pascal") is showing the pascal matrix of order 3.
- So users can change the order of the matrix also.
Examples
- 1.MATRIX("pascal") =1
- 2.MATRIX("pascal",3)
| 1 | 1 | 1 |
| 1 | 2 | 3 |
| 1 | 3 | 6 |
- 3.MATRIX("pascal",5)
| 1 | 1 | 1 | 1 | 1 |
| 1 | 2 | 3 | 4 | 5 |
| 1 | 3 | 6 | 10 | 15 |
| 1 | 4 | 10 | 20 | 35 |
| 1 | 5 | 15 | 35 | 70 |
 is the size of the Pascal matrix.
is the size of the Pascal matrix.

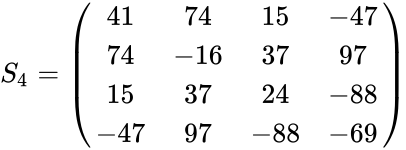
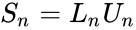 .
.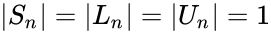
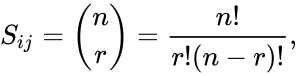 , where n=i+j, r=i.
, where n=i+j, r=i.
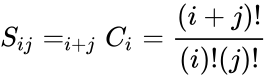 .
.