Difference between revisions of "Manuals/calci/PENTADIAGONAL"
Jump to navigation
Jump to search
| Line 22: | Line 22: | ||
==Examples== | ==Examples== | ||
| − | *1.MATRIX("pentadiagonal") | + | *1.MATRIX("pentadiagonal") =22 |
| + | *2.MATRIX("pentadiagonal",3) | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Line 31: | Line 32: | ||
| 21 || -25 || -64 | | 21 || -25 || -64 | ||
|} | |} | ||
| − | * | + | *3.MATRIX("pentadiagonal",6) |
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Line 46: | Line 47: | ||
| 0 || 0 || 0 || -43 || 19 || 89 | | 0 || 0 || 0 || -43 || 19 || 89 | ||
|} | |} | ||
| − | * | + | *4.MATRIX("pentadiagonal:negative",4) |
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Line 57: | Line 58: | ||
| 0 || -12.941046571359038 || -31.090207281522453 || -52.342877350747585 | | 0 || -12.941046571359038 || -31.090207281522453 || -52.342877350747585 | ||
|} | |} | ||
| − | * | + | *5.MATRIX("pentadiagonal:positive",5) |
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Line 70: | Line 71: | ||
| 0 || 0 || 32.176876766607165 || 47.92787255719304 || 48.10425683390349 | | 0 || 0 || 32.176876766607165 || 47.92787255719304 || 48.10425683390349 | ||
|} | |} | ||
| − | + | ||
==See Also== | ==See Also== | ||
*[[Manuals/calci/SYMMETRIC| SYMMETRIC]] | *[[Manuals/calci/SYMMETRIC| SYMMETRIC]] | ||
Latest revision as of 01:33, 26 October 2015
MATRIX("PENTADIAGONAL",order)
- is the size of the Pentadiagonal matrix.
Description
- This function gives the pentadiagonal matrix of order 3.
- A pentadiagonal matrix is a matrix that is nearly diagonal.
- So it is a matrix in which the only nonzero entries are on the main diagonal, and the first two diagonals above and below it.
- The form of pentadiagonal matrix is:
.
- When n is the size of the matrix, a pentadiagonal matrix has atmost 5n-6 nonzero entries.
- Here MATIRX("pentadiagonal") is showing the penta diagonal matrix of order 3 with the integer numbers.
- Also in Calci users can get a deimal values with positive and negative numbers.
- The syntax is to get the decimal penta diagonal matrix is MATRIX("pentadiagonal:negative") and MATRIX(pentadiagonal:positive")
Examples
- 1.MATRIX("pentadiagonal") =22
- 2.MATRIX("pentadiagonal",3)
| -58 | 15 | -4 |
| -54 | 55 | -75 |
| 21 | -25 | -64 |
- 3.MATRIX("pentadiagonal",6)
| 54 | -56 | -28 | 0 | 0 | 0 |
| 62 | -96 | -82 | -49 | 0 | 0 |
| 15 | 23 | 20 | 30 | 94 | 0 |
| 0 | 80 | 95 | 76 | -82 | 66 |
| 0 | 0 | -60 | -27 | -82 | -87 |
| 0 | 0 | 0 | -43 | 19 | 89 |
- 4.MATRIX("pentadiagonal:negative",4)
| -59.92012487258762 | -79.75753229111433 | -20.13208125717938 | 0 |
| -47.0609312877059 | -7.832704461179674 | -29.973211092874408 | -12.44902245234698 |
| -47.85296192858368 | -67.0970072504133 | -53.094227402471006 | -84.4662182033062 |
| 0 | -12.941046571359038 | -31.090207281522453 | -52.342877350747585 |
- 5.MATRIX("pentadiagonal:positive",5)
| 86.68749532662332 | 69.28418821189553 | 15.4073191806674 | 0 | 0 |
| 35.21442376077175 | 31.06112303212285 | 35.75007226318121 | 77.74382838979363 | 0 |
| 24.096227367408574 | 42.69053868483752 | 98.5696179093793 | 5.866385693661869 | 81.69623236171901 |
| 0 | 80.96880922093987 | 67.79956801328808 | 45.05093654152006 | 71.03362120687962 |
| 0 | 0 | 32.176876766607165 | 47.92787255719304 | 48.10425683390349 |
 is the size of the Pentadiagonal matrix.
is the size of the Pentadiagonal matrix.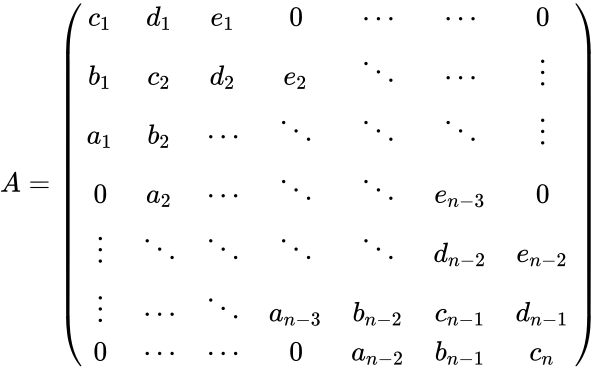 .
.