Difference between revisions of "Manuals/calci/TOEPLITZ"
Jump to navigation
Jump to search
| (4 intermediate revisions by 2 users not shown) | |||
| Line 21: | Line 21: | ||
==Examples== | ==Examples== | ||
| − | *MATRIX("toeplitz", | + | *MATRIX("toeplitz") =0.5239269779995084 |
| + | *MATRIX("toeplitz",3) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 0.5852752963546664|| 0.5083035423886031 || 0.8240970941260457 | ||
| + | |- | ||
| + | | 0.5852752963546664 || 0.5852752963546664 || 0.5083035423886031 | ||
| + | |- | ||
| + | | 0.5083035423886031 || 0.5852752963546664 || 0.585275296354666 | ||
| + | |} | ||
| + | *MATRIX("toeplitz",5,1..7) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 1 || 2 || 3 || 4 || 5 | ||
| + | |- | ||
| + | | 6 || 1 || 2 || 3 || 4 | ||
| + | |- | ||
| + | | 7 || 6 || 1 || 2 || 3 | ||
| + | |- | ||
| + | | 1 || 7 || 6 || 1 || 2 | ||
| + | |- | ||
| + | | 2 || 1 || 7 || 6 || 1 | ||
| + | |} | ||
| + | *MATRIX("toeplitz",4,761..770) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 761 || 762 || 763 || 764 | ||
| + | |- | ||
| + | | 765 || 761 || 762 || 763 | ||
| + | |- | ||
| + | | 766 || 765 || 761 || 762 | ||
| + | |- | ||
| + | | 767 || 766 || 765 || 761 | ||
| + | |} | ||
| + | ==Related Videos== | ||
| − | + | {{#ev:youtube|CgfkEUOFAj0|280|center|Toeplitz Matix}} | |
| − | + | ||
| − | + | ==See Also== | |
| − | + | *[[Manuals/calci/PERSYMMETRIC| PERSYMMETRIC]] | |
| − | + | *[[Manuals/calci/PASCAL| PASCAL]] | |
| − | + | *[[Manuals/calci/TRIANGULAR| TRIANGULAR]] | |
| − | + | ||
| − | + | ==References== | |
| − | + | *[http://en.wikipedia.org/wiki/Toeplitz_matrix Toeplitz Matrix] | |
Latest revision as of 01:43, 26 October 2015
MATRIX("TOEPLITZ",order)
- is the size of the Toeplitz matrix.
Description
- This function gives the matrix of order 3 with the property of toeplitz matrix.
- A Toeplitz matrix is a matrix with the constant values along negative sloping diagonals(descending diagonal from left to right).
- If the i,j element of A is denoted , then we have
.
- Any nxn matrix A of the form:
- The property of Toeplitz matrix is :Toeplitz matrices are persymmetric.
- Symmetric Toeplitz matrices are both centrosymmetric and bisymmetric.
- Toeplitz matrices commute asymptotically.
Examples
- MATRIX("toeplitz") =0.5239269779995084
- MATRIX("toeplitz",3)
| 0.5852752963546664 | 0.5083035423886031 | 0.8240970941260457 |
| 0.5852752963546664 | 0.5852752963546664 | 0.5083035423886031 |
| 0.5083035423886031 | 0.5852752963546664 | 0.585275296354666 |
- MATRIX("toeplitz",5,1..7)
| 1 | 2 | 3 | 4 | 5 |
| 6 | 1 | 2 | 3 | 4 |
| 7 | 6 | 1 | 2 | 3 |
| 1 | 7 | 6 | 1 | 2 |
| 2 | 1 | 7 | 6 | 1 |
- MATRIX("toeplitz",4,761..770)
| 761 | 762 | 763 | 764 |
| 765 | 761 | 762 | 763 |
| 766 | 765 | 761 | 762 |
| 767 | 766 | 765 | 761 |
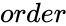 is the size of the Toeplitz matrix.
is the size of the Toeplitz matrix.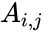 , then we have
, then we have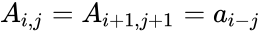 .
.
