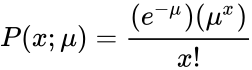Difference between revisions of "Manuals/calci/POISSONDISTRIBUTION"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> '''RANDOMNUMBERGENERATION'''(Number, RandomNumber, Distribution, NewTableFlag, Lambda) where, '''Number '''-...") |
|||
| (7 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''POISSONDISTRIBUTED(a,b)'''</div><br/> |
| + | *<math>a</math> is the number of random numbers to display. | ||
| − | + | ==Description== | |
| + | *This function shows the random variables of Poisson distribution. | ||
| + | *It is a discrete frequency distribution which gives the probability of a number of independent events occurring in a fixed time. | ||
| + | *A Poisson random variable is the number of successes that result from a Poisson experiment. | ||
| + | *The probability distribution of a Poisson random variable is called a Poisson distribution. | ||
| + | *Suppose we conduct a Poisson experiment, in which the average number of successes within a given region is <math>\mu</math>. | ||
| + | *Then, the Poisson probability is: | ||
| + | <math>P(x;\mu) = \frac{(e^{-\mu}) (\mu^x)}{ x!}</math> | ||
| + | *where x is the actual number of successes that result from the experiment, and e is approximately equal to 2.71828. | ||
| + | *The Poisson distribution has the following properties: | ||
| + | #The mean of the distribution is equal to <math>\mu</math> . | ||
| + | #The variance is also equal to <math>\mu</math> . | ||
| + | *This function will give the result as error when b<0 and a value is not an integer. | ||
| − | + | ==Examples== | |
| + | #POISSONDISTRIBUTED(2,3) = 2 4 | ||
| + | #POISSONDISTRIBUTED(7,23) = 23 26 22 22 24 23 20 | ||
| + | #POISSONDISTRIBUTED(3,-7) = Null | ||
| − | + | ==See Also== | |
| + | *[[Manuals/calci/poisson | poisson ]] | ||
| + | *[[Manuals/calci/EXPONDIST | EXPONDIST ]] | ||
| − | + | ==References== | |
| − | + | [http://stattrek.com/probability-distributions/poisson.aspx Poisson Probability Distribution ] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 06:56, 27 October 2015
POISSONDISTRIBUTED(a,b)
- is the number of random numbers to display.
Description
- This function shows the random variables of Poisson distribution.
- It is a discrete frequency distribution which gives the probability of a number of independent events occurring in a fixed time.
- A Poisson random variable is the number of successes that result from a Poisson experiment.
- The probability distribution of a Poisson random variable is called a Poisson distribution.
- Suppose we conduct a Poisson experiment, in which the average number of successes within a given region is .
- Then, the Poisson probability is:
- where x is the actual number of successes that result from the experiment, and e is approximately equal to 2.71828.
- The Poisson distribution has the following properties:
- The mean of the distribution is equal to .
- The variance is also equal to .
- This function will give the result as error when b<0 and a value is not an integer.
Examples
- POISSONDISTRIBUTED(2,3) = 2 4
- POISSONDISTRIBUTED(7,23) = 23 26 22 22 24 23 20
- POISSONDISTRIBUTED(3,-7) = Null
 is the number of random numbers to display.
is the number of random numbers to display.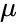 .
.