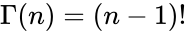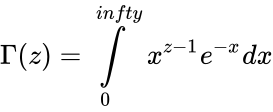Difference between revisions of "Manuals/calci/GAMMAFUNCTION"
Jump to navigation
Jump to search
| Line 9: | Line 9: | ||
*Gamma function is defined for all complex numbers except the non-positive integers. | *Gamma function is defined for all complex numbers except the non-positive integers. | ||
*For complex numbers with a positive real part, it is defined via a convergent improper integral: | *For complex numbers with a positive real part, it is defined via a convergent improper integral: | ||
| − | <math>\Gamma (z) = \int\limits_{0}^{ | + | <math>\Gamma (z) = \int\limits_{0}^{infty} x^{z-1} e^{-x} dx </math> |
Revision as of 15:00, 28 November 2016
GAMMAFUNCTION (z)
- is any positive real number.
Description
- This function gives the value of the Gamma function.
- The Gamma function is defined to be an extension of the factorial to complex and real number arguments.
- That is, if n is a positive integer:
- Gamma function is defined for all complex numbers except the non-positive integers.
- For complex numbers with a positive real part, it is defined via a convergent improper integral:
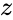 is any positive real number.
is any positive real number.