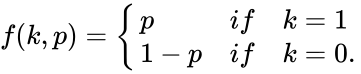Difference between revisions of "Manuals/calci/BERNOULLIDISTRIBUTED"
Jump to navigation
Jump to search
| Line 13: | Line 13: | ||
*The <math>Probability</math> vaule is ranges from 0 to 1. | *The <math>Probability</math> vaule is ranges from 0 to 1. | ||
*The Bernoulli distribution is defined by:<math>f(x)=p^x(1-p)^{1-x} </math> for x={0,1}, where p is the probability that a particular event will occur. | *The Bernoulli distribution is defined by:<math>f(x)=p^x(1-p)^{1-x} </math> for x={0,1}, where p is the probability that a particular event will occur. | ||
| − | *The probability mass function is :math>f(k,p) = \begin{cases}p &if& k=1\\ | + | *The probability mass function is :<math>f(k,p) = \begin{cases}p &if& k=1\\ |
1-p &if &k=0. | 1-p &if &k=0. | ||
\end{cases}</math> | \end{cases}</math> | ||
Revision as of 13:56, 7 December 2016
BERNOULLIDISTRIBUTED (Numbers,Probability)
- is the number of variables.
- is the value range from 0 to 1.
Description
- This function gives the value of the Bernoulli distribution.
- It is a discrete probability distribution.
- Bernoulli distribution is the theoretical distribution of the number of successes in a finite set of independent trials with a constant probability of success.
- The Bernoulli distribution is simply BINOM(1,P).
- This distribution best describes all situations where a trial is made resulting in either success or failure, such as when tossing a coin, or when modeling the success or failure.
- In , represents the number of variables.
- is the probability value.
- The vaule is ranges from 0 to 1.
- The Bernoulli distribution is defined by: for x={0,1}, where p is the probability that a particular event will occur.
- The probability mass function is :
- This function will give the result as error when
1. Any one of the argument is nonnumeric. 2. The value of p<0 or p>1.
 is the number of variables.
is the number of variables. is the value range from 0 to 1.
is the value range from 0 to 1. ,
,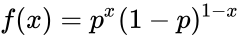 for x={0,1}, where p is the probability that a particular event will occur.
for x={0,1}, where p is the probability that a particular event will occur.