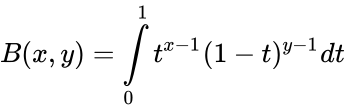Difference between revisions of "Manuals/calci/BETAFUNCTION"
Jump to navigation
Jump to search
| Line 6: | Line 6: | ||
*Beta function is also called the Euler integral of the first kind. | *Beta function is also called the Euler integral of the first kind. | ||
*To evaluate the Beta function we usually use the Gamma function. | *To evaluate the Beta function we usually use the Gamma function. | ||
| − | <math>B(x,y)=\frac{Gamma(x)Gamma(y)}{Gamma(x+y)}</math>. | + | <math>B(x,y)=\frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}</math>. |
*For x,y positive we define the Beta function by: | *For x,y positive we define the Beta function by: | ||
<math>B(x,y)= \int\limits_{0}^{1} t^{x-1}(1-t)^{y-1} dt</math> | <math>B(x,y)= \int\limits_{0}^{1} t^{x-1}(1-t)^{y-1} dt</math> | ||
Revision as of 15:44, 7 December 2016
BETAFUNCTION (a,b)
- and are any positive real numbers.
Description
- This function returns the value of the Beta function.
- Beta function is also called the Euler integral of the first kind.
- To evaluate the Beta function we usually use the Gamma function.
.
- For x,y positive we define the Beta function by:
 and
and  are any positive real numbers.
are any positive real numbers.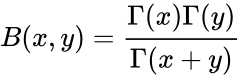 .
.