Difference between revisions of "Manuals/calci/KFUNCTION"
Jump to navigation
Jump to search
| Line 10: | Line 10: | ||
*The K-Function is given as : | *The K-Function is given as : | ||
<math>L(d)=\frac{\sqrt{A \sum_{i=1}^n \sum_{j=1,j\neq i}^n k(i,j)}}{\pi n(n-1)}</math> | <math>L(d)=\frac{\sqrt{A \sum_{i=1}^n \sum_{j=1,j\neq i}^n k(i,j)}}{\pi n(n-1)}</math> | ||
| + | Where d is the distance, n is equal to the total number of features. | ||
| + | *<math>A</math> represents the total area of the features and <math>k_{i,j}</math> is a weight. | ||
| + | *If there is no edge correction, then the weight will be equal to one when the distance between i and j is less than d, and will equate to zero otherwise. | ||
| + | |||
| + | ==Examples== | ||
| + | # KFUNCTION(5) = 27648 | ||
| + | # KFUNCTION(5) = 2.157794122294186e+34 | ||
| + | # KFUNCTION(6.453) = 86400000 | ||
| + | |||
| + | ==See Also== | ||
| + | |||
| + | *[[Manuals/calci/SUM | SUM]] | ||
| + | *[[Manuals/calci/SQRT | SQRT]] | ||
| + | |||
| + | ==References== | ||
| + | [http://resources.esri.com/help/9.3/arcgisdesktop/com/gp_toolref/spatial_statistics_tools/how_multi_distance_spatial_cluster_analysis_colon_ripley_s_k_function_spatial_statistics_works.htm K Function] | ||
Revision as of 14:45, 14 December 2016
KFUNCTION (Number)
- is any real number.
Description
- This function shows the value of the K function.
- In ,Number is any real number.
- K function is named as Ripley's K Function.
- It is defined as how the spatial clustering or dispersion of feature centroids changes when the neighborhood size changes.
- When using this tool, specify the number of distances to evaluate and, optionally, a starting distance and/or distance increment.
- The K-Function is given as :
Where d is the distance, n is equal to the total number of features.
- represents the total area of the features and is a weight.
- If there is no edge correction, then the weight will be equal to one when the distance between i and j is less than d, and will equate to zero otherwise.
Examples
- KFUNCTION(5) = 27648
- KFUNCTION(5) = 2.157794122294186e+34
- KFUNCTION(6.453) = 86400000
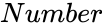 is any real number.
is any real number.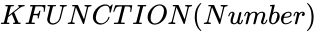 ,Number is any real number.
,Number is any real number.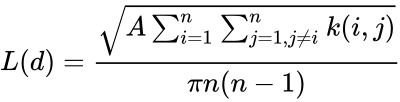
 represents the total area of the features and
represents the total area of the features and 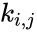 is a weight.
is a weight.