Difference between revisions of "Manuals/calci/POISSON"
Jump to navigation
Jump to search
(Created page with "==poisson") |
|||
| Line 1: | Line 1: | ||
| − | == | + | <div style="font-size:30px">'''POISSON(x,m,cu)'''</div><br/> |
| + | *<math>x</math> is the number of events. | ||
| + | *<math>m </math> is the mean | ||
| + | *<math>cu</math> is the logical value like TRUE or FALSE. | ||
| + | |||
| + | ==Description== | ||
| + | *This function gives the value of the Poisson distribution. | ||
| + | *The Poisson distribution is a discrete probability distribution for the counts of events that occur randomly in a given interval of time. | ||
| + | *It is is used to model the number of events occurring within a given time interval. | ||
| + | *In <math>POISSON(x,m,cu)</math>, <math>x</math> is the number of events in a given interval of time, <math>m </math> is the Average Numeric value and <math>cu</math> is the logical value. | ||
| + | *If it is TRUE, this function will give the Cumulative Poisson Probability with the number of random events between <math>0</math> and <math>x</math>(included). | ||
| + | *If it is FALSE, this function will give the Poisson Probability Mass function with the number of events occurring will be exactly <math>x</math>. | ||
| + | *The <math>POISSON</math>probability mass function is: | ||
| + | <math> f(x,\lambda)=\frac{\lambda^x.e^{-\lambda}}{x!}</math> | ||
| + | <math>x=0,1,2...</math> where <math> \lambda </math> is the shape parameter and <math>\lambda > 0</math>. <math>e</math> is the base of the natural logarithm (e=2.718282). | ||
| + | *The Cumulative Poisson Probability function is: | ||
| + | <math>F(k,\lambda)=\sum_{k=0}^x \frac{e^{-\lambda} .\lambda^k}{k!}</math>. | ||
| + | *This function will return the result as error when | ||
| + | 1.<math>x</math> or <math>m</math> is non-numeric. | ||
| + | 2.<math>x<0</math> or <math>m<0</math>. | ||
| + | |||
| + | ==Examples== | ||
| + | #POISSON(10,3,TRUE) = 0.9997076630493528 | ||
| + | #POISSON(10,3,FALSE) = 0.0008101511794681433 | ||
| + | #POISSON(21.7,7.54,TRUE) = 0.9999955033358848 | ||
| + | #POISSON(21.7,7.54,FALSE) = 0.00000948031184308478 | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/EXPONDIST | EXPONDIST ]] | ||
| + | |||
| + | ==References== | ||
| + | [http://en.wikipedia.org/wiki/Poisson_distribution Poisson distribution ] | ||
Revision as of 13:35, 15 December 2016
POISSON(x,m,cu)
- is the number of events.
- is the mean
- is the logical value like TRUE or FALSE.
Description
- This function gives the value of the Poisson distribution.
- The Poisson distribution is a discrete probability distribution for the counts of events that occur randomly in a given interval of time.
- It is is used to model the number of events occurring within a given time interval.
- In , is the number of events in a given interval of time, is the Average Numeric value and is the logical value.
- If it is TRUE, this function will give the Cumulative Poisson Probability with the number of random events between and (included).
- If it is FALSE, this function will give the Poisson Probability Mass function with the number of events occurring will be exactly .
- The probability mass function is:
where is the shape parameter and . is the base of the natural logarithm (e=2.718282).
- The Cumulative Poisson Probability function is:
.
- This function will return the result as error when
1. or is non-numeric. 2. or .
Examples
- POISSON(10,3,TRUE) = 0.9997076630493528
- POISSON(10,3,FALSE) = 0.0008101511794681433
- POISSON(21.7,7.54,TRUE) = 0.9999955033358848
- POISSON(21.7,7.54,FALSE) = 0.00000948031184308478
 is the number of events.
is the number of events.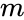 is the mean
is the mean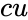 is the logical value like TRUE or FALSE.
is the logical value like TRUE or FALSE.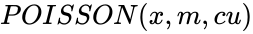 ,
, 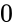 and
and  probability mass function is:
probability mass function is:
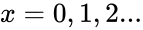 where
where 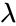 is the shape parameter and
is the shape parameter and  .
. 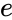 is the base of the natural logarithm (e=2.718282).
is the base of the natural logarithm (e=2.718282).
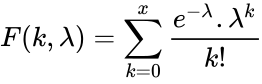 .
.
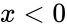 or
or  .
.