Difference between revisions of "Manuals/calci/SKEWSYMMETRIC"
Jump to navigation
Jump to search
| Line 7: | Line 7: | ||
*A Skew Symmetric is a square matrix which satisfies the following identity <math>A=A^T</math>,where <math>A^T</math> is the matrix transpose. | *A Skew Symmetric is a square matrix which satisfies the following identity <math>A=A^T</math>,where <math>A^T</math> is the matrix transpose. | ||
*If the entry in the <math>i^{th}</math> row and <math>j^{th}</math> column is <math>a_{ij}</math>. | *If the entry in the <math>i^{th}</math> row and <math>j^{th}</math> column is <math>a_{ij}</math>. | ||
| − | *i.e.<math>A = (a_{ij})</math> then the skew symmetric condition is <math>a_{ij} = | + | *i.e.<math>A = (a_{ij})</math> then the skew symmetric condition is <math>(a_{ij}) = −(a_{ij})</math>. |
*So its diagonal values are "0". | *So its diagonal values are "0". | ||
Revision as of 14:47, 20 December 2016
SKEWSYMMETRIC(Order)
- is the order of the skew symmetric matrix.
Description
- This function shows the Skew Symmetric matrix with the given order.
- Skew Symmetric is also called Anti Symmetric or Antimetric.
- A Skew Symmetric is a square matrix which satisfies the following identity ,where is the matrix transpose.
- If the entry in the row and column is .
- i.e. then the skew symmetric condition is Failed to parse (syntax error): {\displaystyle (a_{ij}) = −(a_{ij})} .
- So its diagonal values are "0".
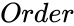 is the order of the skew symmetric matrix.
is the order of the skew symmetric matrix.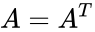 ,where
,where 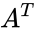 is the matrix transpose.
is the matrix transpose.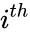 row and
row and 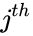 column is
column is 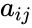 .
.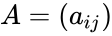 then the skew symmetric condition is Failed to parse (syntax error): {\displaystyle (a_{ij}) = −(a_{ij})}
.
then the skew symmetric condition is Failed to parse (syntax error): {\displaystyle (a_{ij}) = −(a_{ij})}
.