Difference between revisions of "Manuals/calci/SKEWSYMMETRIC"
Jump to navigation
Jump to search
| Line 11: | Line 11: | ||
==Examples== | ==Examples== | ||
| − | #SKEWSYMMETRIC(4) | + | #1. |
| + | SKEWSYMMETRIC(4) | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Line 22: | Line 23: | ||
|(-25) || -72 || -43 || 0 | |(-25) || -72 || -43 || 0 | ||
|} | |} | ||
| + | #2. | ||
| + | SKEWSYMMETRIC(9) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 0 || 48|| -36 || 72 || 25 ||51 ||-13 || -98 || 70 | ||
| + | |- | ||
| + | |(-48) || 0 || -97|| -33 || 78 || -30 || -56 || 62 || 45 | ||
| + | |- | ||
| + | |36|| 97 || 0 ||42 || -47 || 58 || 94 || 24 || -43 | ||
| + | |- | ||
| + | |(-72) || 33 || -42 || 0 || -23 || -77 || -80 || 69 || 70 | ||
| + | |- | ||
| + | | (-25) || -78 || 47 || 23 || 0 || -17 || 17 || -100 || 34 | ||
| + | |- | ||
| + | | (-51) || 30 || -58 || 77 || 17 || 0 || -43 || -67 || 0 | ||
| + | |- | ||
| + | |13 || 56 || -94 || 80 || -17 || 43 || 0 || -24 || 55 | ||
| + | |- | ||
| + | | 98 || -62 || -24 || -69 || 100 || 67 || 24 || 0 || 76 | ||
| + | |- | ||
| + | | (-70) || -45 || 43 || -70 || -34 || 0 || -55 || -76 || 0 | ||
| + | |} | ||
| + | 0 48 -36 72 25 51 -13 -98 70 | ||
| + | -48 0 -97 -33 78 -30 -56 62 45 | ||
| + | 36 97 0 42 -47 58 94 24 -43 | ||
| + | -72 33 -42 0 -23 -77 -80 69 70 | ||
| + | -25 -78 47 23 0 -17 17 -100 34 | ||
| + | -51 30 -58 77 17 0 -43 -67 0 | ||
| + | 13 56 -94 80 -17 43 0 -24 55 | ||
| + | 98 -62 -24 -69 100 67 24 0 76 | ||
| + | -70 -45 43 -70 -34 0 -55 -76 0 | ||
Revision as of 15:13, 20 December 2016
SKEWSYMMETRIC(Order)
- is the order of the skew symmetric matrix.
Description
- This function shows the Skew Symmetric matrix with the given order.
- Skew Symmetric is also called Anti Symmetric or Antimetric.
- A Skew Symmetric is a square matrix which satisfies the following identity ,where is the matrix transpose.
- If the entry in the row and column is .
- i.e. then the skew symmetric condition is Failed to parse (syntax error): {\displaystyle (a_{ij}) = −(a_{ij})} .
- So its diagonal values are "0".
Examples
- 1.
SKEWSYMMETRIC(4)
| 0 | -39 | 2 | 25 |
| 39 | 0 | 15 | 72 |
| (-2) | -15 | 0 | 43 |
| (-25) | -72 | -43 | 0 |
- 2.
SKEWSYMMETRIC(9)
| 0 | 48 | -36 | 72 | 25 | 51 | -13 | -98 | 70 |
| (-48) | 0 | -97 | -33 | 78 | -30 | -56 | 62 | 45 |
| 36 | 97 | 0 | 42 | -47 | 58 | 94 | 24 | -43 |
| (-72) | 33 | -42 | 0 | -23 | -77 | -80 | 69 | 70 |
| (-25) | -78 | 47 | 23 | 0 | -17 | 17 | -100 | 34 |
| (-51) | 30 | -58 | 77 | 17 | 0 | -43 | -67 | 0 |
| 13 | 56 | -94 | 80 | -17 | 43 | 0 | -24 | 55 |
| 98 | -62 | -24 | -69 | 100 | 67 | 24 | 0 | 76 |
| (-70) | -45 | 43 | -70 | -34 | 0 | -55 | -76 | 0 |
0 48 -36 72 25 51 -13 -98 70 -48 0 -97 -33 78 -30 -56 62 45 36 97 0 42 -47 58 94 24 -43 -72 33 -42 0 -23 -77 -80 69 70 -25 -78 47 23 0 -17 17 -100 34 -51 30 -58 77 17 0 -43 -67 0 13 56 -94 80 -17 43 0 -24 55 98 -62 -24 -69 100 67 24 0 76 -70 -45 43 -70 -34 0 -55 -76 0
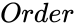 is the order of the skew symmetric matrix.
is the order of the skew symmetric matrix.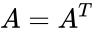 ,where
,where 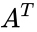 is the matrix transpose.
is the matrix transpose. row and
row and 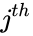 column is
column is 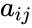 .
.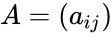 then the skew symmetric condition is Failed to parse (syntax error): {\displaystyle (a_{ij}) = −(a_{ij})}
.
then the skew symmetric condition is Failed to parse (syntax error): {\displaystyle (a_{ij}) = −(a_{ij})}
.