Difference between revisions of "Manuals/calci/ZTESTEQUALMEANS"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> '''ZTESTTWOSAMPLEFORMEANS('''Array1, Array2, Variance1, Variance2, Alpha, NewTableFlag) where, '''Array1 '''-...") |
|||
| (16 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''ZTESTTWOSAMPLEFORMEANS(ar1,ar2,v1,v2,md,alpha,lv)'''</div><br/> |
| + | *<math>ar1</math> and <math>ar2</math> are array of values. | ||
| + | *<math>v1</math> and <math>v2</math> are value of variances. | ||
| + | *<math>md</math> is the Hypothesized Mean Difference. | ||
| + | *<math>alpha</math> is the significance level. | ||
| + | *<math>lv</math> is the logical value. | ||
| − | + | ==Description== | |
| + | *This function gives the z-test two sample for means. | ||
| + | *We can use this test when | ||
| + | 1.The samples can be different sizes. | ||
| + | 2.The two samples are independent. | ||
| + | 3.Both populations are normally distributed or both sample sizes are large enough that the means are normally distributed. | ||
| + | *In <math> ZTESTTWOSAMPLEFORMEANS(ar_1,ar_2,v_1,v_2,md,alpha,lv)</math>,<math> ar_1 </math> and <math>ar_2</math> are the set of values,<math>v_1</math> is the variance of <math>ar_1</math>,<math>v_2</math> is the variance of <math>ar_2</math>. | ||
| + | *<math> md </math> is the Hypothesized Mean Difference. If testing is for equal means,then <math>md = 0</math>. | ||
| + | *<math>alpha</math> is the significance level which ranges from 0 to 1. | ||
| + | *<math>lv</math> is the logical value like TRUE or FALSE.TRUE is indicating the result will display in new worksheet. | ||
| + | *Suppose we are omitted the <math>lv</math> value it will consider the value as FALSE. | ||
| + | *ZTEST two sample for means is calculated by:<math> z=\frac{\bar{x_1}-\bar{x_2}-\Delta}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}</math> | ||
| + | where <math>\bar{x_1}</math> and <math>\bar{x_2}</math> are average of two samples, <math>\Delta</math> is the Hypothesized Mean Difference between two means of the population. <math>\sigma_1</math> and <math>\sigma_2</math> are the standard deviation of two population. <math>n_1</math> and <math>n_2</math> are the sizes of the samples. | ||
| + | *This function will give the result as error when | ||
| + | 1. any one of the argument is nonnumeric. | ||
| + | 2. alpha>1 | ||
| − | + | ==Examples== | |
| + | #'''Example 1''' | ||
| + | {| class="wikitable" | ||
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! !! A !! B | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 70.25 || 90.02 | ||
| + | |- | ||
| + | ! 2 | ||
| + | | 82.87 || 89.45 | ||
| + | |- | ||
| + | ! 3 | ||
| + | | 90.17 || 70.89 | ||
| + | |- | ||
| + | ! 4 | ||
| + | | 45.55 || 107.91 | ||
| + | |- | ||
| + | ! 5 | ||
| + | | 51.98 || 59.09 | ||
| + | |- | ||
| + | ! 6 | ||
| + | | 21.28 || 45.03 | ||
| + | |- | ||
| + | ! 7 | ||
| + | | 39.04 || 56.08 | ||
| + | |- | ||
| + | ! 8 | ||
| + | | 40.47 || 91 | ||
| + | |- | ||
| + | ! 9 | ||
| + | | 30.02 || 40.41 | ||
| + | |- | ||
| + | ! 10 | ||
| + | | 100.05 || 29.04 | ||
| + | |- | ||
| + | ! 11 | ||
| + | | 86.1 || 37.79 | ||
| + | |- | ||
| + | ! 12 | ||
| + | | 72.49 || 41.07 | ||
| + | |- | ||
| + | ! 13 | ||
| + | | 29.54 || 52.04 | ||
| + | |- | ||
| + | ! 14 | ||
| + | | 38.76 || 60.78 | ||
| + | |- | ||
| + | ! 15 | ||
| + | | 47.01 || 66.06 | ||
| + | |- | ||
| + | ! 16 | ||
| + | | 50.65 || 78.01 | ||
| + | |- | ||
| + | ! 17 | ||
| + | | 55.91 || 41.22 | ||
| + | |- | ||
| + | ! 18 | ||
| + | | 102.7 || 33.99 | ||
| + | |- | ||
| + | ! 19 | ||
| + | | 10 || 110.02 | ||
| + | |} | ||
| + | #=ZTESTTWOSAMPLEFORMEANS(A1:A18,B1:B19,641.8474654,630.283176,0,0.5) | ||
| − | + | {| class="wikitable" | |
| − | + | |+Result | |
| − | + | |- | |
| − | + | |+z-TEST: TWO SAMPLE FOR MEANS | |
| − | + | |- | |
| − | + | ! !! VARIABLE1 !!VARIABLE2 | |
| − | + | |- | |
| − | + | |MEAN || 56.04421052631579||63.152631578947364 | |
| − | + | |- | |
| − | + | | KNOWN VARIANCE || 641.8474654||630.283176 | |
| − | + | |- | |
| − | + | |OBSERVATIONS ||19||19 | |
| − | + | |- | |
| − | + | | HYPOTHESIZED MEAN DIFFERENCE ||0 | |
| − | + | |- | |
| − | + | |z VALUE ||-0.8687285374505475 | |
| − | + | |- | |
| − | + | | P(T<=+t) ONE-TAIL|| 0.1924981032229391 | |
| − | + | |- | |
| − | + | |z CRITICAL ONE-TAIL || 0 | |
| − | + | |- | |
| − | + | |P(T<=t) TWO-TAIL ||0.3849962064458782 | |
| − | + | |- | |
| − | + | |z CRITICAL TWO-TAIL|| 0.6744897501960817 | |
| − | < | + | |} |
| − | |||
| − | |||
| − | |||
| − | |||
| − | - | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==Related Videos== | |
| − | + | {{#ev:youtube|gJZNpfrjYEA|280|center|Z-TEST Two Sample For Means}} | |
| − | - | ||
| − | |||
| − | + | ==See Also== | |
| − | + | *[[Manuals/calci/ZTEST| ZTEST]] | |
| − | + | *[[Manuals/calci/TTEST| TTEST]] | |
| − | + | *[[Manuals/calci/TINV| TINV]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==References== | |
| − | ---- | + | *[http://www.cliffsnotes.com/math/statistics/univariate-inferential-tests/two-sample-z-test-for-comparing-two-means Ztest Comparing two means] |
Latest revision as of 14:02, 16 January 2017
ZTESTTWOSAMPLEFORMEANS(ar1,ar2,v1,v2,md,alpha,lv)
- and are array of values.
- and are value of variances.
- is the Hypothesized Mean Difference.
- is the significance level.
- is the logical value.
Description
- This function gives the z-test two sample for means.
- We can use this test when
1.The samples can be different sizes. 2.The two samples are independent. 3.Both populations are normally distributed or both sample sizes are large enough that the means are normally distributed.
- In , and are the set of values, is the variance of , is the variance of .
- is the Hypothesized Mean Difference. If testing is for equal means,then .
- is the significance level which ranges from 0 to 1.
- is the logical value like TRUE or FALSE.TRUE is indicating the result will display in new worksheet.
- Suppose we are omitted the value it will consider the value as FALSE.
- ZTEST two sample for means is calculated by:
where and are average of two samples, is the Hypothesized Mean Difference between two means of the population. and are the standard deviation of two population. and are the sizes of the samples.
- This function will give the result as error when
1. any one of the argument is nonnumeric. 2. alpha>1
Examples
- Example 1
| A | B | |
|---|---|---|
| 1 | 70.25 | 90.02 |
| 2 | 82.87 | 89.45 |
| 3 | 90.17 | 70.89 |
| 4 | 45.55 | 107.91 |
| 5 | 51.98 | 59.09 |
| 6 | 21.28 | 45.03 |
| 7 | 39.04 | 56.08 |
| 8 | 40.47 | 91 |
| 9 | 30.02 | 40.41 |
| 10 | 100.05 | 29.04 |
| 11 | 86.1 | 37.79 |
| 12 | 72.49 | 41.07 |
| 13 | 29.54 | 52.04 |
| 14 | 38.76 | 60.78 |
| 15 | 47.01 | 66.06 |
| 16 | 50.65 | 78.01 |
| 17 | 55.91 | 41.22 |
| 18 | 102.7 | 33.99 |
| 19 | 10 | 110.02 |
- =ZTESTTWOSAMPLEFORMEANS(A1:A18,B1:B19,641.8474654,630.283176,0,0.5)
| VARIABLE1 | VARIABLE2 | |
|---|---|---|
| MEAN | 56.04421052631579 | 63.152631578947364 |
| KNOWN VARIANCE | 641.8474654 | 630.283176 |
| OBSERVATIONS | 19 | 19 |
| HYPOTHESIZED MEAN DIFFERENCE | 0 | |
| z VALUE | -0.8687285374505475 | |
| P(T<=+t) ONE-TAIL | 0.1924981032229391 | |
| z CRITICAL ONE-TAIL | 0 | |
| P(T<=t) TWO-TAIL | 0.3849962064458782 | |
| z CRITICAL TWO-TAIL | 0.6744897501960817 |
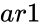 and
and 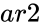 are array of values.
are array of values.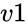 and
and 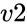 are value of variances.
are value of variances.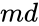 is the Hypothesized Mean Difference.
is the Hypothesized Mean Difference.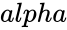 is the significance level.
is the significance level. is the logical value.
is the logical value.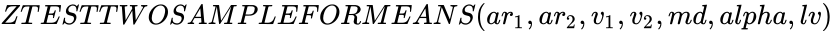 ,
,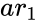 and
and 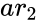 are the set of values,
are the set of values,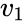 is the variance of
is the variance of 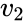 is the variance of
is the variance of 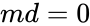 .
.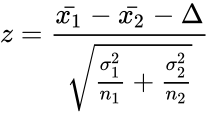
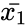 and
and 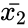 are average of two samples,
are average of two samples,  is the Hypothesized Mean Difference between two means of the population.
is the Hypothesized Mean Difference between two means of the population. 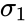 and
and 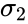 are the standard deviation of two population.
are the standard deviation of two population. 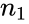 and
and 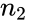 are the sizes of the samples.
are the sizes of the samples.