Difference between revisions of "Manuals/calci/LOGNORMDIST"
Jump to navigation
Jump to search
| Line 45: | Line 45: | ||
==References== | ==References== | ||
[http://en.wikipedia.org/wiki/Log-normal_distribution Log-normal distribution] | [http://en.wikipedia.org/wiki/Log-normal_distribution Log-normal distribution] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Revision as of 01:30, 13 March 2017
LOGNORMDIST(number,mean,standarddeviation)
- is the value.
- is the mean value of ,
- is the standard deviation value of .
Description
- This function gives the value of the cumulative log normal distribution.
- This distribution is the continuous probability distribution.
- Lognomal distribution is also called Galton's distribution.
- A random variable which is log-normally distributed takes only positive real values.
- Suppose is Normally Distributed function, then also Normally Distributed
- also Normally Distributed.
- Let the Normal Distribution function and its Mean= , Standard Deviation =
- Then the lognormal cumulative distribution is calculated by:
where is the error function,. The error function (also called the Gauss error function) is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations.
- And is the Cumulative Distribution function of the Standard Normal distribution.
- This function will give the result as error when
1. Any one of the argument is non-numeric. 2. Suppose or
ZOS
- The syntax is to calculate cumulative log normal distribution in ZOS is .
- is the value.
- is the mean value of .
- is the standard deviation value of .
- For e.g.,LOGNORMDIST(10,8.002,4.501)
Examples
- =LOGNORMDIST(2,5.4,2.76) = 0.044061652
- =LOGNORMDIST(10,24.05,12.95) = 0.046543186
- =LOGNORMDIST(50,87.0036,42.9784) = 0.026597569
- =LOGNORMDIST(-10,5,2) = NAN
Related Videos
See Also
References
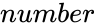 is the value.
is the value.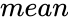 is the mean value of
is the mean value of 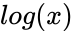 ,
,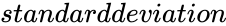 is the standard deviation value of
is the standard deviation value of  is Normally Distributed function, then
is Normally Distributed function, then 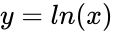 also Normally Distributed
also Normally Distributed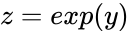 also Normally Distributed.
also Normally Distributed.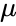 , Standard Deviation =
, Standard Deviation = 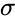
![{\displaystyle F(x,\mu ,\sigma )={\frac {1}{2}}\left[1+erf\left({\frac {ln(x)-\mu )}{\sigma {\sqrt {2}}}}\right)\right]=\varphi \left[{\frac {ln(x)-\mu }{\sigma }}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/png/52b64b4678d5c128bfb328f7005a734bed36e0b6) where
where 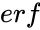 is the error function,. The error function (also called the Gauss error function) is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations.
is the error function,. The error function (also called the Gauss error function) is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations.
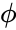 is the Cumulative Distribution function of the Standard Normal distribution.
is the Cumulative Distribution function of the Standard Normal distribution.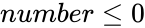 or
or 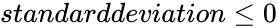
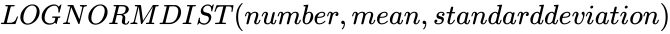 .
.