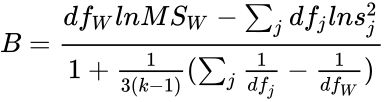Difference between revisions of "Bartlett'sTest"
Jump to navigation
Jump to search
| Line 9: | Line 9: | ||
* That is, if the samples come from non-normal distributions, then Bartlett's test may simply be testing for non-normality. | * That is, if the samples come from non-normal distributions, then Bartlett's test may simply be testing for non-normality. | ||
<math>B=\frac{df_WlnMS_W-\sum_{j}df_jln s_j^2}{1+\frac{1}{3(k-1)}(\sum_{j}\frac{1}{df_j}-\frac{1}{df_W})}</math> | <math>B=\frac{df_WlnMS_W-\sum_{j}df_jln s_j^2}{1+\frac{1}{3(k-1)}(\sum_{j}\frac{1}{df_j}-\frac{1}{df_W})}</math> | ||
| + | * B is the Bartlett's test static. | ||
| + | * <math<MS_W</math> is the pooled variance across all groups. | ||
Revision as of 07:46, 9 May 2017
BARTLETTSTEST(DataRange,ConfidenceLevel,NewTableFlag)
- is the array of x values.
- is the value from 0 to 1.
- is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.
Description
- Bartlett's test is used to test if k samples are from populations with equal variances.
- Bartlett's test is sensitive to departures from normality.
- That is, if the samples come from non-normal distributions, then Bartlett's test may simply be testing for non-normality.
- B is the Bartlett's test static.
- <math<MS_W</math> is the pooled variance across all groups.
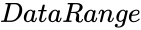 is the array of x values.
is the array of x values.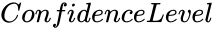 is the value from 0 to 1.
is the value from 0 to 1.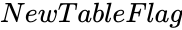 is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.
is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.