Difference between revisions of "Manuals/calci/MATRIXDETERMINANT"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''MATRIXDETERMINANT (a)'''</div><br/> *<math> a </math> is any square matrix. ==Description== *This function is calculating the determinant of th...") |
|||
| Line 37: | Line 37: | ||
<math>|A|=\sum_{j=1}^n a_{ij} A_{ij}</math>, for any fixed <math>i</math>. | <math>|A|=\sum_{j=1}^n a_{ij} A_{ij}</math>, for any fixed <math>i</math>. | ||
Also<math>|A|=\sum_{i=1}^n a_{ij} A_{ij}</math>, for any fixed <math>j</math>. | Also<math>|A|=\sum_{i=1}^n a_{ij} A_{ij}</math>, for any fixed <math>j</math>. | ||
| + | |||
| + | ==Examples== | ||
| + | #MATRIXDETERMINANT([[6,4,8],[3,6,1],[2,4,5]]) = 104.00000000000001 | ||
| + | #MATRIXDETERMINANT([[8,-4],[12,5]]) =88 | ||
| + | #MATRIXDETERMINANT([1,2,3,4;5,6,-7,8;12,10,-13,15;11,7,5,3]) = 1514 | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/MINVERSE | MINVERSE ]] | ||
| + | *[[Manuals/calci/MMULT | MMULT ]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://en.wikipedia.org/wiki/Determinant Determinant ] | ||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | *[[ Z3 | Z3 home ]] | ||
Revision as of 15:23, 14 June 2017
MATRIXDETERMINANT (a)
- is any square matrix.
Description
- This function is calculating the determinant of the given matrix.
- In , is any square matrix.
- The determinant of a matrix is a special number that can be calculated from a square matrix.
- The determinant of a matrix is denoted by or .
- Let be 2x2 matrix with the elements
- Then , where all are real numbers.
- Let be the 3x3 matrix with the elements
Then :
- Let be a square matrix of order . Write ,
- Where is the entry on the row and column and to & to .
- For any and , set (called the co-factors), then the general formula for determinant of the matrix is,
, for any fixed . Also, for any fixed .
Examples
- MATRIXDETERMINANT([[6,4,8],[3,6,1],[2,4,5]]) = 104.00000000000001
- MATRIXDETERMINANT([[8,-4],[12,5]]) =88
- MATRIXDETERMINANT([1,2,3,4;5,6,-7,8;12,10,-13,15;11,7,5,3]) = 1514
 is any square matrix.
is any square matrix.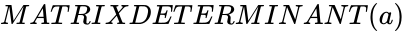 ,
, 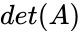 or
or 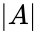 .
. be 2x2 matrix with the elements
be 2x2 matrix with the elements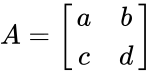
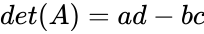 , where
, where 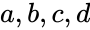 all are real numbers.
all are real numbers.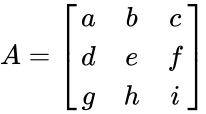 Then
Then 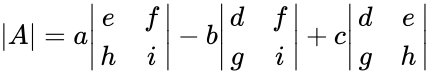 :
:
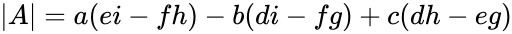
 . Write
. Write 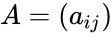 ,
,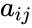 is the entry on the
is the entry on the 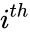 row and
row and 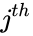 column and
column and 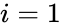 to
to 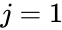 to
to  and
and 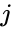 , set
, set 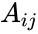 (called the co-factors), then the general formula for determinant of the matrix
(called the co-factors), then the general formula for determinant of the matrix 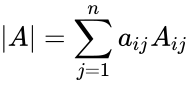 , for any fixed
, for any fixed 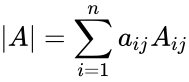 , for any fixed
, for any fixed