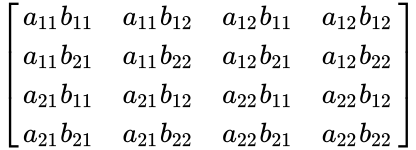Difference between revisions of "Manuals/calci/MATRIXTENSORPRODUCT"
Jump to navigation
Jump to search
| Line 39: | Line 39: | ||
\end{bmatrix} </math> = | \end{bmatrix} </math> = | ||
<math>\begin{bmatrix} | <math>\begin{bmatrix} | ||
| − | a_{11}b_{11} a_{11}b_{12} a_{12}b_{11} | + | a_{11}b_{11} & a_{11}b_{12} & a_{12}b_{11} & a_{12}b_{12}\\ |
| + | a_{11}b_{21} & a_{11}b_{22} & a_{12}b_{21} & a_{12}b_{22}\\ | ||
| + | a_{21}b_{11} & a_{21}b_{12} & a_{22}b_{11} & a_{22}b_{12}\\ | ||
| + | a_{21}b_{21} & a_{21}b_{22} & a_{22}b_{21} & a_{22}b_{22} | ||
\end{bmatrix} </math> | \end{bmatrix} </math> | ||
Revision as of 13:45, 12 July 2017
MATRIXTENSORPRODUCT (a,b)
- and are any two matrices.
Description
- This function shows the Tensor product of the matrix.
- In , and are any two matrices.
- Here matrices and should be square matrix with same order.
- Tensor product is denoted by .
- Tensor product is different from general product.
- The Tensor product is defined by the product two vector spaces V and W is itself a Vector space.
- It is denoted by .
- The tensor product of V and W is the vector space generated by the symbols , with and .
- The tensor product from the direct sum vector space, whose dimension is the sum of the dimensions of the two summands:
- Now consider any 2x2 matrices:
=
 and
and  are any two matrices.
are any two matrices.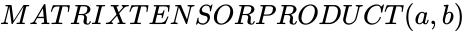 ,
,  .
.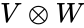 .
.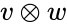 , with
, with 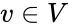 and
and 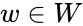 .
.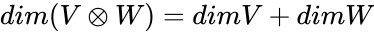
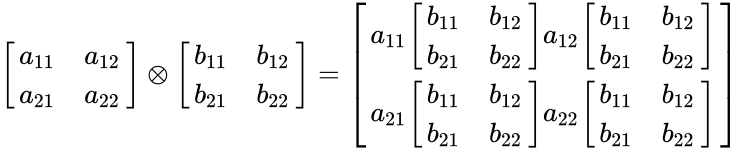 =
=