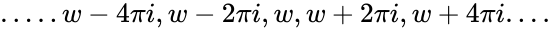Difference between revisions of "Manuals/calci/IMLOG"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''IMLOG (ComplexNumber,Base)'''</div><br/> *<math>ComplexNumber</math> is any complex number. *<math>Base</math> is the base value of the Log. ==...") |
|||
| Line 11: | Line 11: | ||
*Thus, a logarithm of a complex number z is a complex number w such that <math>e^w = z</math>. | *Thus, a logarithm of a complex number z is a complex number w such that <math>e^w = z</math>. | ||
*The notation for such a <math>w</math> is <math>ln z</math> or <math>log z</math>. | *The notation for such a <math>w</math> is <math>ln z</math> or <math>log z</math>. | ||
| − | *If <math>z = re^{ | + | *If <math>z = re^{i\theta}</math> with <math>r > 0</math>which is in Polar form, then <math>w = ln r + i\theta</math> is one logarithm of z. |
*Adding integer multiples of 2πi gives all the others. | *Adding integer multiples of 2πi gives all the others. | ||
*The complex exponential function is not injective, because <math>e^{w+2\pi i} = e^w</math> for any w, since adding iθ to w has the effect of rotating <math>e^w</math> counterclockwise θ radians. | *The complex exponential function is not injective, because <math>e^{w+2\pi i} = e^w</math> for any w, since adding iθ to w has the effect of rotating <math>e^w</math> counterclockwise θ radians. | ||
*So the points <math>.....w-4\pi i,w-2 \pi i, w, w+2\pi i,w+4 \pi i....</math> | *So the points <math>.....w-4\pi i,w-2 \pi i, w, w+2\pi i,w+4 \pi i....</math> | ||
Revision as of 16:54, 2 August 2017
IMLOG (ComplexNumber,Base)
- is any complex number.
- is the base value of the Log.
Description
- This function shows the log value of a complex number.
- In , is any complex number.
- is the base value of a Log values.
- A complex logarithm function is an "inverse" of the complex exponential function.
- It is same as the real natural logarithm ln x is the inverse of the real exponential function.
- Thus, a logarithm of a complex number z is a complex number w such that .
- The notation for such a is or .
- If with which is in Polar form, then is one logarithm of z.
- Adding integer multiples of 2πi gives all the others.
- The complex exponential function is not injective, because for any w, since adding iθ to w has the effect of rotating counterclockwise θ radians.
- So the points
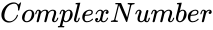 is any complex number.
is any complex number.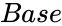 is the base value of the Log.
is the base value of the Log.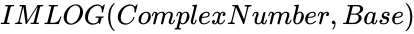 ,
,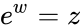 .
.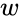 is
is 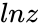 or
or 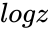 .
.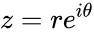 with
with 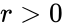 which is in Polar form, then
which is in Polar form, then 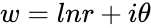 is one logarithm of z.
is one logarithm of z.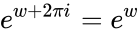 for any w, since adding iθ to w has the effect of rotating
for any w, since adding iθ to w has the effect of rotating 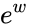 counterclockwise θ radians.
counterclockwise θ radians.