Difference between revisions of "Manuals/calci/QRDECOMPOSITION"
Jump to navigation
Jump to search
| Line 7: | Line 7: | ||
*QR Decomposition is also called QR Factorization. | *QR Decomposition is also called QR Factorization. | ||
*QR Decomposition is defined by the product of Orthogonal matrix and Upper Triangular matrix. | *QR Decomposition is defined by the product of Orthogonal matrix and Upper Triangular matrix. | ||
| − | *Consider any square matrix A may be decomposed as <math>A=QR</math>,where <math>Q</math> stands for orthogonal matrix and <math>R</math> stands for Upper Triangular matrix. | + | *Consider any square matrix A may be decomposed as <math>A=QR</math>, where <math>Q</math> stands for orthogonal matrix and <math>R</math> stands for Upper Triangular matrix. |
| − | *An orthogonal matrix should satisfy <math>Q^TQ=I</math>,where <math>I</math> is identity or Unitary matrix. | + | *An orthogonal matrix should satisfy <math>Q^TQ=I</math>, where <math>I</math> is identity or Unitary matrix. |
*<math>Q^T</math> is the transpose matrix of Q. | *<math>Q^T</math> is the transpose matrix of Q. | ||
| − | *If the given matrix A is non singular, then this factorization is unique. | + | *If the given matrix A is non-singular, then this factorization is unique. |
*Gram-Schmidt process is one of the process of computing decomposition in QR Decomposition method. | *Gram-Schmidt process is one of the process of computing decomposition in QR Decomposition method. | ||
Revision as of 04:48, 4 September 2017
QRDECOMPOSITION (Matrix)
- is the set of values.
Description
- This function gives the value of QR Decomposition.
- In , is any matrix.
- QR Decomposition is also called QR Factorization.
- QR Decomposition is defined by the product of Orthogonal matrix and Upper Triangular matrix.
- Consider any square matrix A may be decomposed as , where stands for orthogonal matrix and stands for Upper Triangular matrix.
- An orthogonal matrix should satisfy , where is identity or Unitary matrix.
- is the transpose matrix of Q.
- If the given matrix A is non-singular, then this factorization is unique.
- Gram-Schmidt process is one of the process of computing decomposition in QR Decomposition method.
Examples
1. QRDECOMPOSITION([[2,6],[10,-15]])
-0.19611613513818393 -0.9805806756909202 |
-0.9805806756909202 0.19611613513818393 |
-10.19803902718557 13.5320133245347 |
-1.1102230246251565e-15 -8.825226081218279 |
2. QRDECOMPOSITION([[3,8,-5],[4,-6.3,9],[2,5,-1]])
-0.5570860145311556 0.631547425332445 -0.5392615524675877 |
-0.7427813527082074 -0.669329688618384 -0.01654176541311622 | -0.3713906763541037 0.3913382392381005 0.841975859527614 |
| -5.385164807134504 -1.634118975958056 -3.528211425363985 |
-2.1551618871879059e-16 11.22584763714588 -9.573042563465782 |
5.3446973501217775e-17 0 1.7054560140922779 |
See Also
 is the set of values.
is the set of values. ,
,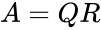 , where
, where  stands for orthogonal matrix and
stands for orthogonal matrix and 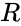 stands for Upper Triangular matrix.
stands for Upper Triangular matrix.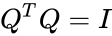 , where
, where 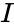 is identity or Unitary matrix.
is identity or Unitary matrix.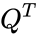 is the transpose matrix of Q.
is the transpose matrix of Q.