Difference between revisions of "Manuals/calci/BINOMIAL"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> '''RANDOMNUMBERGENERATION'''(Number, RandomNumber, Distribution, NewTableFlag, ProbabilityValue,Trials) where, ...") |
|||
| (7 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''BINOMIAL(N,K)'''</div><br/> |
| + | *<math>N</math> is the number of items. | ||
| + | *<math>K </math> is the number of selection. | ||
| − | |||
| − | where, | + | ==Description== |
| + | *This function gives the coefficent of the binomial distribution. | ||
| + | *Binomial coefficient is the set of positive integer which equals the number of combinations of k items that can be selected from a set of n items. | ||
| + | *The coefficients satisfy the Pascals recurrence. | ||
| + | *The binomial coefficents are denoted by <math>\binom{n}{k}</math> and it is read by n choose k. | ||
| + | *It is the coefficient of the <math>x^k</math> term in the polynomial expansion of the binomial thorem <math>(1 + x)^n</math>. | ||
| + | *The coefficient is occur in the formula of binomial thorem: | ||
| + | <math>(x+y)^n=\sum _{k=0}^n \binom{n}{k} x^{n-k} y^k</math> where <math> k\le n</math>. | ||
| + | *To find the coefficient of the binomial ,we can use several methods. | ||
| + | 1. Recursive formula | ||
| + | 2. Multiplicative formula | ||
| + | 3. Factorial formula. | ||
| + | *1.Recursive Formula: | ||
| + | <math>\binom{n}{k}= \binom{n-1}{k-1} +\binom{n-1}{k}</math> for <math>n,k>0</math> and <math>1\le k\le n-1</math>. | ||
| + | *2. Multiplicative formula: | ||
| + | <math>\binom{n}{k}= \prod_{i=1}^k \frac{n+1-i}{i}</math> | ||
| + | *3.Factorial formula: | ||
| + | <math>\binom{n}{k}= \frac{n!}{k!(n-k)!}</math> where <math>k\le n</math>,and which is zero when <math>k>n</math>. | ||
| + | *Also for the initial values <math> \binom{n}{0}=\binom{n}{n}=1 </math> for <math>n\ge 0</math>. | ||
| + | *Most compact formula for the coefficient of the binomial value is Factorial formula. | ||
| + | *Factorial formula is symmetric of the combination formula. | ||
| − | + | ==ZOS== | |
| − | + | *The syntax is to calculate BINOMIAL in ZOS is <math>BINOMIAL (N,K)</math>. | |
| + | **<math>N</math> is the number of items. | ||
| + | **<math>K</math> is the number of selection. | ||
| + | *For e.g., BINOMIAL(20..25,4) | ||
| + | *BINOMIAL(10..14,7..8) | ||
| − | + | ==Examples== | |
| + | #=BINOMIAL(10,3)= 120 | ||
| + | #=BINOMIAL(20,7)= 77520 | ||
| + | #=BINOMIAL(15,0)= 1 | ||
| + | #=BINOMIAL(12,12)=1 | ||
| + | #=BINOMIAL(1,-1) = 0 | ||
| − | + | ==Related Videos== | |
| − | + | {{#ev:youtube|tWIa6Dovirs|280|center|BINOMIAL}} | |
| − | + | ==See Also== | |
| + | *[[Manuals/calci/BINOMDIST | BINOMDIST ]] | ||
| + | *[[Manuals/calci/BINOMDIST | BINOMIALDIST ]] | ||
| − | + | ==References== | |
| − | + | *[http://en.wikipedia.org/wiki/Binomial_distribution Binomial Distribution] | |
| − | + | *[http://en.wikipedia.org/wiki/Binomial_coefficient Binomial Coefficient] | |
| − | |||
| − | |||
| − | |||
| − | + | *[[Z_API_Functions | List of Main Z Functions]] | |
| − | + | *[[ Z3 | Z3 home ]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 14:11, 5 June 2018
BINOMIAL(N,K)
- is the number of items.
- is the number of selection.
Description
- This function gives the coefficent of the binomial distribution.
- Binomial coefficient is the set of positive integer which equals the number of combinations of k items that can be selected from a set of n items.
- The coefficients satisfy the Pascals recurrence.
- The binomial coefficents are denoted by and it is read by n choose k.
- It is the coefficient of the term in the polynomial expansion of the binomial thorem .
- The coefficient is occur in the formula of binomial thorem:
where .
- To find the coefficient of the binomial ,we can use several methods.
1. Recursive formula 2. Multiplicative formula 3. Factorial formula.
- 1.Recursive Formula:
for and .
- 2. Multiplicative formula:
- 3.Factorial formula:
where ,and which is zero when .
- Also for the initial values for .
- Most compact formula for the coefficient of the binomial value is Factorial formula.
- Factorial formula is symmetric of the combination formula.
ZOS
- The syntax is to calculate BINOMIAL in ZOS is .
- is the number of items.
- is the number of selection.
- For e.g., BINOMIAL(20..25,4)
- BINOMIAL(10..14,7..8)
Examples
- =BINOMIAL(10,3)= 120
- =BINOMIAL(20,7)= 77520
- =BINOMIAL(15,0)= 1
- =BINOMIAL(12,12)=1
- =BINOMIAL(1,-1) = 0
Related Videos
See Also
References
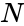 is the number of items.
is the number of items.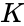 is the number of selection.
is the number of selection.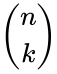 and it is read by n choose k.
and it is read by n choose k.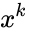 term in the polynomial expansion of the binomial thorem
term in the polynomial expansion of the binomial thorem 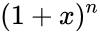 .
.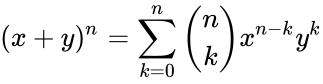 where
where 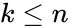 .
.
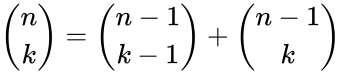 for
for 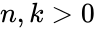 and
and  .
.
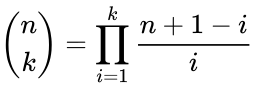
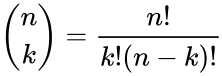 where
where 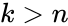 .
.
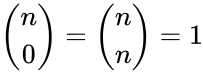 for
for 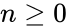 .
.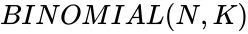 .
.