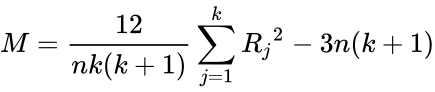Difference between revisions of "Manuals/calci/FRIEDMANTEST"
Jump to navigation
Jump to search
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:25px">''' | + | <div style="font-size:25px">'''FRIEDMANTEST (SampleDataByGroup,ConfidenceLevel,NewTableFlag)'''</div><br/> |
| − | *<math> | + | *<math>SampleDataByGroup</math> is the array of values to find the test statistic. |
| − | *<math> | + | *<math>ConfidenceLevel</math> is the value between 0 and 1. |
| − | *<math> | + | *<math>NewTableFlag</math> is either TRUE or FALSE. |
==Description== | ==Description== | ||
| Line 189: | Line 189: | ||
| − | [[Z_API_Functions | List of Main Z Functions]] | + | *[[Z_API_Functions | List of Main Z Functions]] |
| − | [[ Z3 | Z3 home ]] | + | *[[ Z3 | Z3 home ]] |
Latest revision as of 12:19, 6 June 2018
FRIEDMANTEST (SampleDataByGroup,ConfidenceLevel,NewTableFlag)
- is the array of values to find the test statistic.
- is the value between 0 and 1.
- is either TRUE or FALSE.
Description
- This function gives the Test statistic summary of FriedMan Test.
- Friedman's test is a nonparametric test that compares three or more paired groups.
- It is the alternative to ANOVA with repeated measures.
- It is used to test for differences between groups when the dependent variable being measured is ordinal.
- It can also be used for continuous data that has violated the assumptions necessary to run the one-way ANOVA with repeated measures.
- This test is simelar to the Kruskal Wallis test.
- The data of the Fried Man test having the following assumptions:
- 1. One group that is measured on three or more different occasions.
- 2.Group is a random sample from the population.
- 3.The dependent variable should be measured at the ordinal or continuous level.
- 4.Samples do not need to be normally distributed.
- Steps for Fried man Test:
- 1.Define Null and Alternative Hypotheses:Null Hypotheses:There is no difference between the conditions.Alternative Hypotheses:There is a difference between the conditions.
- 2.State Alpha:Alpha=0.05.
- 3.Calculate degrees of freedom:df = k – 1, where k = number of groups.
- 4.State Decision Rule:From the Chi squared table calculate the critical value.
- Suppose the chisquared(symbol)is greater than the critical value then reject the null hypothesis
- 5.Calculate the Test Statistic:
- k = number of columns (often called “treatments”)
- n = number of rows (often called “blocks”)
- Rj = sum of the ranks in column j.
- If there is no significant difference between the sum of the ranks of each of the columns, then M will be small, but if at least one column shows significant difference then M will be larger.
- 6.State Results:In this step we have to take a decision of null hypothesis either accept or reject depending on the critical value table.
- 7.State Conclusion:To be significant, our obtained U has to be equal to or LESS than this
critical value.
Example
| White | Red | Rose |
| 10 | 7 | 8 |
| 8 | 5 | 5 |
| 7 | 8 | 6 |
| 9 | 6 | 4 |
| 7 | 5 | 7 |
| 4 | 7 | 5 |
| 5 | 9 | 3 |
| 6 | 6 | 7 |
| 5 | 4 | 6 |
| 10 | 6 | 4 |
| 4 | 7 | 4 |
| 7 | 3 | 3 |
- =FRIEDMANTEST(A1:C13,0.05,TRUE)
| White | Red | Rose |
|---|---|---|
| 3 | 1 | 2 |
| 3 | 1.5 | 1.5 |
| 2 | 3 | 1 |
| 3 | 2 | 1 |
| 2.5 | 1 | 2.5 |
| 1 | 3 | 2 |
| 2 | 3 | 1 |
| 1.5 | 1.5 | 3 |
| 2 | 1 | 3 |
| 3 | 2 | 1 |
| 1.5 | 3 | 1.5 |
| 3 | 1.5 | 1.5 |
| ANALYSIS | |||
|---|---|---|---|
| White | Red | Rose | |
| Sum Of Ranks | 27.5 | 23.5 | 21 |
| SS | 756.25 | 552.25 | 441 |
| Qr | 1.7916666666666572 | ||
| df | 2 | ||
| AsymSig | 0.4082672341468858 |
Related Videos
See Also
References
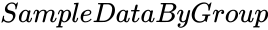 is the array of values to find the test statistic.
is the array of values to find the test statistic.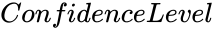 is the value between 0 and 1.
is the value between 0 and 1.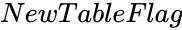 is either TRUE or FALSE.
is either TRUE or FALSE.