Difference between revisions of "Manuals/calci/BETAINV"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
| − | <div style="font-size: | + | <div style="font-size:25px">'''BETAINV (Probability,Alpha,Beta,LowerBound,UpperBound,Accuracy,DivisionsAndDepthArray)'''</div><br/> |
*<math>Probability</math> is the probability value associated with the beta distribution. | *<math>Probability</math> is the probability value associated with the beta distribution. | ||
*<math>Alpha</math> & <math>Beta</math> are the values of the shape parameter. | *<math>Alpha</math> & <math>Beta</math> are the values of the shape parameter. | ||
| Line 9: | Line 9: | ||
*In <math>BETAINV (Probability,Alpha,Beta,LowerBound,UpperBound,Accuracy,DivisionsAndDepthArray)</math>, <math>Probability</math> is the probability value associated with Beta Distribution, <math>Alpha</math> and <math>Beta</math> are the values of two positive shape parameters and <math>LowerBound</math> and <math>UpperBound</math> are the lower and upper limit. | *In <math>BETAINV (Probability,Alpha,Beta,LowerBound,UpperBound,Accuracy,DivisionsAndDepthArray)</math>, <math>Probability</math> is the probability value associated with Beta Distribution, <math>Alpha</math> and <math>Beta</math> are the values of two positive shape parameters and <math>LowerBound</math> and <math>UpperBound</math> are the lower and upper limit. | ||
*Normally the limit values are optional, i.e. when we are giving the values of <math>LowerBound</math>&<math>UpperBound</math> then the result value is from <math>a</math> and <math>b</math>. | *Normally the limit values are optional, i.e. when we are giving the values of <math>LowerBound</math>&<math>UpperBound</math> then the result value is from <math>a</math> and <math>b</math>. | ||
| − | *When we are omitting the values <math> | + | *When we are omitting the values <math>LowerBound</math> and <math>UpperBound</math>, by default it will consider <math>LowerBound=0</math> and <math>UpperBound=1</math>, so the result value is from <math>0</math> and <math>1</math>. |
*If <math>BETADIST (Number,Alpha,Beta,LowerBound,UpperBound)=Probability</math>, then <math>BETAINV (Probability,Alpha,Beta,LowerBound,UpperBound,Accuracy,DivisionsAndDepthArray)=x</math>. | *If <math>BETADIST (Number,Alpha,Beta,LowerBound,UpperBound)=Probability</math>, then <math>BETAINV (Probability,Alpha,Beta,LowerBound,UpperBound,Accuracy,DivisionsAndDepthArray)=x</math>. | ||
*<math>BETAINV</math> use the iterating method to find the value of <math>x</math>.suppose the iteration has not converged after 100 searches, then the function gives the error result. | *<math>BETAINV</math> use the iterating method to find the value of <math>x</math>.suppose the iteration has not converged after 100 searches, then the function gives the error result. | ||
*This function will give the error result when | *This function will give the error result when | ||
1.Any one of the arguments are non-numeric | 1.Any one of the arguments are non-numeric | ||
| − | 2. | + | 2.Alpha or Beta <math>\le</math> 0 |
| − | 3. | + | 3.Number<LowerBound ,Number>UpperBound or LowerBound = UpperBound |
| − | 4.we are not mentioning the limit values for | + | 4.we are not mentioning the limit values for LowerBound & UpperBound , |
by default it will consider the Standard Cumulative Beta Distribution, LowerBound = 0 and UpperBound = 1 | by default it will consider the Standard Cumulative Beta Distribution, LowerBound = 0 and UpperBound = 1 | ||
Revision as of 16:35, 12 June 2018
BETAINV (Probability,Alpha,Beta,LowerBound,UpperBound,Accuracy,DivisionsAndDepthArray)
- is the probability value associated with the beta distribution.
- & are the values of the shape parameter.
- & the lower and upper limit to the interval of .
Description
- This function gives the inverse value of Cumulative Beta Probability Distribution.
- It is called Inverted Beta Function or Beta Prime.
- In , is the probability value associated with Beta Distribution, and are the values of two positive shape parameters and and are the lower and upper limit.
- Normally the limit values are optional, i.e. when we are giving the values of & then the result value is from and .
- When we are omitting the values and , by default it will consider and , so the result value is from and .
- If , then .
- use the iterating method to find the value of .suppose the iteration has not converged after 100 searches, then the function gives the error result.
- This function will give the error result when
1.Any one of the arguments are non-numeric 2.Alpha or Beta 0 3.Number<LowerBound ,Number>UpperBound or LowerBound = UpperBound 4.we are not mentioning the limit values for LowerBound & UpperBound , by default it will consider the Standard Cumulative Beta Distribution, LowerBound = 0 and UpperBound = 1
ZOS
- The syntax is to calculate of this function in ZOS is .
- is the probability value associated with the beta distribution.
- and are the values of the shape parameter.
- For e.g.,BETAINV(0.30987,10,18,12,16)
Examples
- BETAINV(0.2060381025,5,9,2,6) = 3
- BETAINV(0.359492343,8,10) = 1.75
- BETAINV(0.685470581,5,8,2,6) = 3.75
- BETAINV(0.75267,1,7,7,9) = 7.25
- BETAINV(0.5689,-2,4,3,5) = NAN, because .
Related Videos
See Also
References
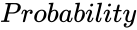 is the probability value associated with the beta distribution.
is the probability value associated with the beta distribution.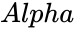 &
& 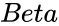 are the values of the shape parameter.
are the values of the shape parameter. &
& 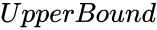 the lower and upper limit to the interval of
the lower and upper limit to the interval of  .
.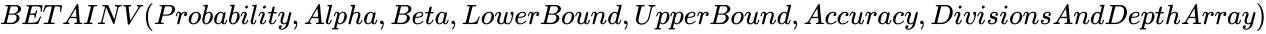 ,
,  and
and 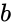 .
.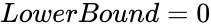 and
and 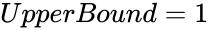 , so the result value is from
, so the result value is from 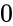 and
and  .
.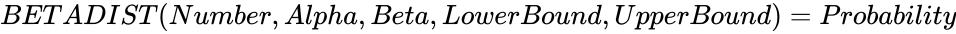 , then
, then 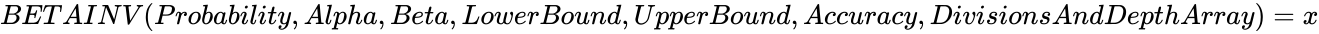 .
. use the iterating method to find the value of
use the iterating method to find the value of 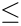 0
3.Number<LowerBound ,Number>UpperBound or LowerBound = UpperBound
4.we are not mentioning the limit values for LowerBound & UpperBound ,
by default it will consider the Standard Cumulative Beta Distribution, LowerBound = 0 and UpperBound = 1
0
3.Number<LowerBound ,Number>UpperBound or LowerBound = UpperBound
4.we are not mentioning the limit values for LowerBound & UpperBound ,
by default it will consider the Standard Cumulative Beta Distribution, LowerBound = 0 and UpperBound = 1
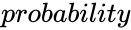 is the probability value associated with the beta distribution.
is the probability value associated with the beta distribution.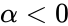 .
.