Difference between revisions of "Manuals/calci/STEYX"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> <font color="#484848"><font face="Arial, sans-serif"><font size="2">'''STEYX'''</font></font></font><font color="#48484...") |
|||
| (15 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''STEYX (KnownYs,KnownXs) '''</div><br/> |
| − | + | *<math>KnownYs</math> is set of dependent values. | |
| − | + | *<math>KnownXs </math> is the set of independent values. | |
| − | + | **STEYX(),returns the standard error of the predicted y-value for each x in the regression. | |
| − | |||
| − | * < | + | ==Description== |
| + | *This function gives the standard error of the regression, which also is known as the standard error of the estimate. | ||
| + | *It is calculates the standard error for the straight line of best fit through a supplied set of <math> KnownXs</math> and <math> KnownYs</math> values. | ||
| + | *The standard error for this line provides a measure of the error in the prediction of <math> KnownYs </math> for an individual <math> KnownXs </math>. | ||
| + | *The equation for the standard error of the predicted <math> y </math> is: | ||
| + | <math>\sqrt{\frac{1}{(n-2)}\left [ \sum(y-\bar{y})^2-\frac{[\sum(x-\bar{x})(y-\bar{y})]^2}{\sum(x-\bar{x})^2} \right ]}</math> | ||
| + | where <math>\bar{x}</math> and <math>\bar{y}</math> are the sample mean <math> x </math> and <math> y </math>. | ||
| + | *In <math>STEYX (KnownYs,KnownXs)</math>, <math>KnownYs </math> is the array of the numeric dependent values and <math> KnownXs </math> is the array of the independent values. | ||
| + | *The arguments can be be either numbers or names, array,constants or references that contain numbers. | ||
| + | *Suppose the array contains text,logical values or empty cells, like that values are not considered. | ||
| + | *This function will return the result as error when | ||
| + | 1. Any one of the argument is non-numeric. | ||
| + | 2. KnownYs and KnownXs are empty or that have less than three data points. | ||
| + | 3. KnownYs and KnownXs have a different number of data points. | ||
| − | + | ==Examples== | |
| − | + | 1. | |
| + | {| class="wikitable" | ||
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! !! A !! B !! C !! D!! E !!F | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 6 || 8 || 10 ||13 || 15 ||5 | ||
| + | |- | ||
| + | ! 2 | ||
| + | | 1 || 4 || 8 || 11 || 20 ||3 | ||
| + | |} | ||
| − | + | =STEYX(A1:F1,A2:F2) = 1.4525201161135368 | |
| + | 2. | ||
| + | {| class="wikitable" | ||
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! !! A !! B !! C !! D!! E | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 2 || 9 || 1 ||8 || 17 | ||
| + | |- | ||
| + | ! 2 | ||
| + | | 10 || 4 || 11 || 2 || 6 | ||
| + | |} | ||
| − | + | =STEYX(A1:E1,A2:E2)) = 5.944184833375669 | |
| − | + | 3. | |
| − | + | {| class="wikitable" | |
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! !! A !! B !! C !! D!! E | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 1 || 2 || 4 ||5 || 8 | ||
| + | |- | ||
| + | ! 2 | ||
| + | | 10 || 4 || 7 || 5 || | ||
| + | |} | ||
| − | STEYX | + | =STEYX(A1:A5,B1:B4) = NAN |
| − | + | ==Related Videos== | |
| − | |||
| − | |||
| − | + | {{#ev:youtube|npmg9yvkz3g|280|center|Standard Error Of Estimate}} | |
| − | + | ==See Also== | |
| + | *[[Manuals/calci/INTERCEPT | INTERCEPT]] | ||
| + | *[[Manuals/calci/LINEST | LINEST ]] | ||
| + | *[[Manuals/calci/PEARSON | PEARSON ]] | ||
| − | + | ==References== | |
| + | *[http://www.ncssm.edu/courses/math/Talks/PDFS/Standard%20Errors%20for%20Regression%20Equations.pdf Standard Error] | ||
| − | |||
| − | |||
| − | |||
| − | + | *[[Z_API_Functions | List of Main Z Functions]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *[[ Z3 | Z3 home ]] | |
| − | |||
Latest revision as of 13:58, 18 June 2018
STEYX (KnownYs,KnownXs)
- is set of dependent values.
- is the set of independent values.
- STEYX(),returns the standard error of the predicted y-value for each x in the regression.
Description
- This function gives the standard error of the regression, which also is known as the standard error of the estimate.
- It is calculates the standard error for the straight line of best fit through a supplied set of and values.
- The standard error for this line provides a measure of the error in the prediction of for an individual .
- The equation for the standard error of the predicted is:
where and are the sample mean and .
- In , is the array of the numeric dependent values and is the array of the independent values.
- The arguments can be be either numbers or names, array,constants or references that contain numbers.
- Suppose the array contains text,logical values or empty cells, like that values are not considered.
- This function will return the result as error when
1. Any one of the argument is non-numeric. 2. KnownYs and KnownXs are empty or that have less than three data points. 3. KnownYs and KnownXs have a different number of data points.
Examples
1.
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | 6 | 8 | 10 | 13 | 15 | 5 |
| 2 | 1 | 4 | 8 | 11 | 20 | 3 |
=STEYX(A1:F1,A2:F2) = 1.4525201161135368
2.
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | 2 | 9 | 1 | 8 | 17 |
| 2 | 10 | 4 | 11 | 2 | 6 |
=STEYX(A1:E1,A2:E2)) = 5.944184833375669
3.
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | 1 | 2 | 4 | 5 | 8 |
| 2 | 10 | 4 | 7 | 5 |
=STEYX(A1:A5,B1:B4) = NAN
Related Videos
See Also
References
 is set of dependent values.
is set of dependent values.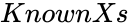 is the set of independent values.
is the set of independent values.
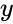 is:
is:![{\displaystyle {\sqrt {{\frac {1}{(n-2)}}\left[\sum (y-{\bar {y}})^{2}-{\frac {[\sum (x-{\bar {x}})(y-{\bar {y}})]^{2}}{\sum (x-{\bar {x}})^{2}}}\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/png/f71cd618f3c8c4c1d1e43f8434dc9778e8b8a697) where
where 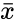 and
and 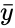 are the sample mean
are the sample mean  and
and  ,
,