Difference between revisions of "Manuals/calci/SERIESSUM"
Jump to navigation
Jump to search
| (7 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''SERIESSUM(x,n,m, | + | <div style="font-size:30px">'''SERIESSUM (x,n,m,coefficients)'''</div><br/> |
*<math>x</math> is the power series value. | *<math>x</math> is the power series value. | ||
*<math>n</math> is the initial power value. | *<math>n</math> is the initial power value. | ||
*<math> m</math> is the step value to increase the n value for each term. | *<math> m</math> is the step value to increase the n value for each term. | ||
| − | *<math> | + | *<math>coefficients</math> is the set of coefficients by which each successive power of x is multiplied. |
| + | **SERIESSUM(), returns the sum of a power series based on the formula. | ||
==Description== | ==Description== | ||
*This function gives the value of the seriessum of the given set of values. | *This function gives the value of the seriessum of the given set of values. | ||
| − | *Seriessum is defined by the following formula : <math>SERIESSUM(x,n,m,a)= | + | *Seriessum is defined by the following formula : <math>SERIESSUM(x,n,m,a)= a_1 x^n + a_2x^{(n+m)} + a_3x^{(n+2m)} +... + a_jx^{(n+(j-1)m)} </math>. |
*Here <math>x</math> is the power-series value, <math>n</math> is the starting power value, <math>m</math> is the increasing value of a power and <math>a</math> is the set of coefficients. | *Here <math>x</math> is the power-series value, <math>n</math> is the starting power value, <math>m</math> is the increasing value of a power and <math>a</math> is the set of coefficients. | ||
*According to the number of coefficients, the number of terms of the power series also get varies. | *According to the number of coefficients, the number of terms of the power series also get varies. | ||
| Line 14: | Line 15: | ||
==Examples== | ==Examples== | ||
| − | #=SERIESSUM(3,2,2, | + | #=SERIESSUM(3,2,2,[1,2,3,4,5,6]) = 3512493 |
| − | #=SERIESSUM(1,0,4, | + | #=SERIESSUM(1,0,4,[1,2,3]) = 6 |
| − | #=SERIESSUM(2,1,5, | + | #=SERIESSUM(2,1,5,[2,4,6,8]) = 536836 |
| − | #=SERIESSUM(0,2,4, | + | #=SERIESSUM(0,2,4,[1,2,3,4,5]) = 0 |
| − | #=SERIESSUM(1,0,3, | + | #=SERIESSUM(1,0,3,[1,2,3,4,5]) = 15 |
| − | #=SERIESSUM(1,1,5, | + | #=SERIESSUM(1,1,5,[1]) = 1 |
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|A6fbDssPeac|280|center|SERIES SUM}} | ||
==See Also== | ==See Also== | ||
| + | *[[Manuals/calci/SUM| SUM]] | ||
| + | *[[Manuals/calci/PRODUCT| PRODUCT]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://en.wikipedia.org/wiki/Series_%28mathematics%29 Series sum] | ||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| − | + | *[[ Z3 | Z3 home ]] | |
Latest revision as of 15:16, 3 July 2018
SERIESSUM (x,n,m,coefficients)
- is the power series value.
- is the initial power value.
- is the step value to increase the n value for each term.
- is the set of coefficients by which each successive power of x is multiplied.
- SERIESSUM(), returns the sum of a power series based on the formula.
Description
- This function gives the value of the seriessum of the given set of values.
- Seriessum is defined by the following formula : .
- Here is the power-series value, is the starting power value, is the increasing value of a power and is the set of coefficients.
- According to the number of coefficients, the number of terms of the power series also get varies.
- For example there 5 values in coefficients, then 5 terms will be there in power series.
This function will give the result as error when any one of the argument is non-numeric.
Examples
- =SERIESSUM(3,2,2,[1,2,3,4,5,6]) = 3512493
- =SERIESSUM(1,0,4,[1,2,3]) = 6
- =SERIESSUM(2,1,5,[2,4,6,8]) = 536836
- =SERIESSUM(0,2,4,[1,2,3,4,5]) = 0
- =SERIESSUM(1,0,3,[1,2,3,4,5]) = 15
- =SERIESSUM(1,1,5,[1]) = 1
Related Videos
See Also
References
 is the power series value.
is the power series value. is the initial power value.
is the initial power value.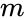 is the step value to increase the n value for each term.
is the step value to increase the n value for each term.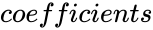 is the set of coefficients by which each successive power of x is multiplied.
is the set of coefficients by which each successive power of x is multiplied.
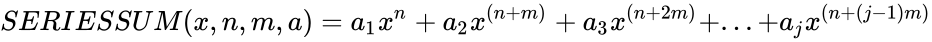 .
. is the set of coefficients.
is the set of coefficients.