Difference between revisions of "Manuals/calci/IMSQRT"
Jump to navigation
Jump to search
| (23 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''IMSQRT( | + | <div style="font-size:30px">'''IMSQRT (ComplexNumber)'''</div><br/> |
| − | *<math> | + | *<math>ComplexNumber </math> is of the form <math>z=x+iy</math>. |
| − | + | **IMSQRT(),returns the difference between two complex numbers | |
==Description== | ==Description== | ||
| − | |||
*This function gives square root of a complex number. | *This function gives square root of a complex number. | ||
| − | *IMSQRT( | + | *IMSQRT(ComplexNumber), where complex number is in the form of "x+iy". |
| − | *where x&y are the real numbers. | + | *where x&y are the real numbers.<math>i</math> imaginary unit .<math>i=\sqrt{-1}</math>. |
| − | *The square root of a complex number is defined by | + | *Consider the complex number z. |
| − | *where r is the modulus of z. <math>r=\sqrt{x^2+y^2}</math> | + | *The square root of a complex number is defined by: |
| − | *And | + | <math>\sqrt{z}=\sqrt{x+iy}=\sqrt{r.e^{i\theta}}=\sqrt{{r}(cos(\frac{\theta}{2})+isin(\frac{\theta}{2})}</math> |
| − | *We can use COMPLEX function to convert real and imaginary number in to a complex number. | + | *where <math>r</math> is the modulus of <math>z</math>. <math>r=\sqrt{x^2+y^2}</math> |
| − | + | *And <math>\theta</math> is the argument of <math>z</math>. <math> \theta=tan^{-1}(y/x)</math> also <math>\theta \isin (-\pi,\pi]</math>. | |
| − | + | *We can use [[Manuals/calci/COMPLEX| COMPLEX]] function to convert real and imaginary number in to a complex number. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | + | ==ZOS== |
| + | *The syntax is to calculate square root of a complex number in ZOS is <math>IMSQRT(ComplexNumber)</math>. | ||
| + | **<math>ComplexNumber</math> is of the form <math>z=x+iy</math> | ||
| + | *For e.g.,IMSQRT("9+10i") | ||
| + | *IMSQRT(IMSUB("9+10i","-2-3i")) | ||
| + | {{#ev:youtube|ofW56najtOE|280|center|Imaginary Square Root}} | ||
| − | + | ==Examples== | |
| + | #=IMSQRT("2+3i")=1.67414922803554+0.895977476129838i | ||
| + | #=IMSQRT("-4-5i")=1.09615788950152-2.2806933416653i | ||
| + | #=IMSQRT("7")=2.6457513110645907+ⅈ0 | ||
| + | #=IMSQRT("8i")=2+2i | ||
| − | + | ==Related Videos== | |
| − | |||
| − | |||
| − | + | {{#ev:youtube|X7Fzk4ijRz8|280|center|IMSQRT}} | |
| − | + | ==See Also== | |
| + | *[[Manuals/calci/IMREAL | IMREAL ]] | ||
| + | *[[Manuals/calci/IMSUM | IMSUM ]] | ||
| + | *[[Manuals/calci/IMAGINARY | IMAGINARY ]] | ||
| + | *[[Manuals/calci/COMPLEX | COMPLEX ]] | ||
| − | |||
| − | |||
| − | |||
| − | + | ==References== | |
| − | + | [http://en.wikipedia.org/wiki/Binary_logarithm Binary Logarithm] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *[[Z_API_Functions | List of Main Z Functions]] | |
| − | + | *[[ Z3 | Z3 home ]] | |
| − | |||
| − | |||
| − | |||
Latest revision as of 15:05, 18 July 2018
IMSQRT (ComplexNumber)
- is of the form .
- IMSQRT(),returns the difference between two complex numbers
Description
- This function gives square root of a complex number.
- IMSQRT(ComplexNumber), where complex number is in the form of "x+iy".
- where x&y are the real numbers. imaginary unit ..
- Consider the complex number z.
- The square root of a complex number is defined by:
- where is the modulus of .
- And is the argument of . also .
- We can use COMPLEX function to convert real and imaginary number in to a complex number.
ZOS
- The syntax is to calculate square root of a complex number in ZOS is .
- is of the form
- For e.g.,IMSQRT("9+10i")
- IMSQRT(IMSUB("9+10i","-2-3i"))
Examples
- =IMSQRT("2+3i")=1.67414922803554+0.895977476129838i
- =IMSQRT("-4-5i")=1.09615788950152-2.2806933416653i
- =IMSQRT("7")=2.6457513110645907+ⅈ0
- =IMSQRT("8i")=2+2i
Related Videos
See Also
References
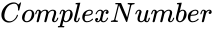 is of the form
is of the form 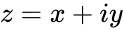 .
.
 imaginary unit .
imaginary unit .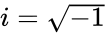 .
.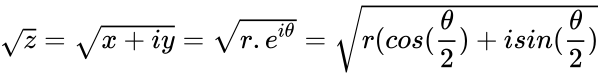
 is the modulus of
is the modulus of 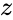 .
. 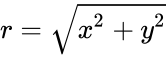
 is the argument of
is the argument of 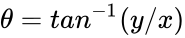 also
also ![{\displaystyle \theta \in (-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/png/2742d923047f035ec3e8db8259485fda0629104b) .
.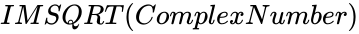 .
.