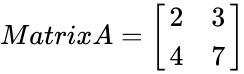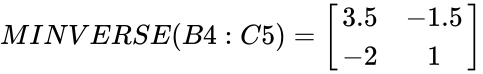Difference between revisions of "Manuals/calci/MINVERSE"
Jump to navigation
Jump to search
| (16 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''MINVERSE( | + | <div style="font-size:30px">'''MINVERSE(a)'''</div><br/> |
| − | *<math> | + | *<math>a</math> is the array of numeric elements. |
| + | **MINVERSE(), returns the matrix inverse of an array. | ||
==Description== | ==Description== | ||
| Line 7: | Line 8: | ||
*1.A matrix must be a square matrix. | *1.A matrix must be a square matrix. | ||
*2.It's determinant not equal to 0. | *2.It's determinant not equal to 0. | ||
| − | *Let <math>A<math> be the 2x2 matrix with the elements A= | + | *Let <math>A</math> be the 2x2 matrix with the elements |
| − | + | <math>A=\begin{bmatrix} | |
| − | *Then the inverse of matrix <math>A<math> is denoted by A^-1. | + | a & b \\ |
| − | + | c & d \\ | |
| − | *Now let A be the matrix is of order nXn. | + | \end{bmatrix}</math>. |
| − | *Then the inverse of A is A^-1= 1 | + | *Then the inverse of matrix <math>A</math> is denoted by <math>A^{-1}</math>. |
| − | *Where adj(A) is the adjoint of A. | + | :<math>A^{-1}=\begin{bmatrix} |
| − | *Adjoint is the matrix formed by taking the | + | a & b \\ |
| − | *Also A.A^-1=A^-1.A=I, where I is the identity matrix.Non-square matrices do not have inverses. | + | c & d \\ |
| + | \end{bmatrix}^{-1}= \frac{1}{ad-bc} * \begin{bmatrix} | ||
| + | d & -b \\ | ||
| + | -c & a \\ | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | *Now let <math>A</math> be the matrix is of order <math>nXn</math>. | ||
| + | *Then the inverse of <math>A</math> is <math>A^{-1}= \frac{1}{det(A)}*adj(A)</math> | ||
| + | *Where <math>adj(A)</math> is the adjoint of <math>A</math>. | ||
| + | *Adjoint is the matrix formed by taking the Transpose of the Co-factor matrix of the original matrix. | ||
| + | *Also <math>A.A^{-1}=A^{-1}.A = I</math>, where <math>I</math> is the identity matrix. | ||
| + | *Non-square matrices do not have inverses. | ||
*Not all square matrices have inverses. | *Not all square matrices have inverses. | ||
*A square matrix which has an inverse is called invertible or non-singular, and a square matrix without an inverse is called non-invertible or singular. | *A square matrix which has an inverse is called invertible or non-singular, and a square matrix without an inverse is called non-invertible or singular. | ||
| Line 22: | Line 34: | ||
2. Suppose number of rows not equal to number of columns | 2. Suppose number of rows not equal to number of columns | ||
| + | ==ZOS== | ||
| + | *The syntax is to calculate the inverse of the matrix in ZOS is <math>MINVERSE(a)</math>. | ||
| + | **<math>a</math> is the array of numeric elements. | ||
| + | *For e.g.,minverse([[10,12],[11,14]]) | ||
== Examples == | == Examples == | ||
| − | Matrix A | + | <math>Matrix A= |
| − | + | \begin{bmatrix} | |
| − | + | 4 & 3 \\ | |
| − | MINVERSE(B5:C6)= | + | 3 & 2 \\ |
| − | + | \end{bmatrix} | |
| − | + | </math> | |
| − | + | <math> | |
| − | + | MINVERSE(B5:C6)= | |
| − | + | \begin{bmatrix} | |
| − | + | -2 & 3 \\ | |
| − | + | 3 & -4 \\ | |
| − | + | \end{bmatrix} | |
| − | + | </math> | |
| − | |||
| + | <math>Matrix A= | ||
| + | \begin{bmatrix} | ||
| + | 3 & 4 \\ | ||
| + | 6 & 8 \\ | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | <math>MINVERSE(C4:D5)=Null</math>, because its determinant value is 0. | ||
| + | |||
| + | <math>Matrix A= | ||
| + | \begin{bmatrix} | ||
| + | 2 & 3 \\ | ||
| + | 4 & 7 \\ | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | <math>MINVERSE(B4:C5)= | ||
| + | \begin{bmatrix} | ||
| + | 3.5 & -1.5 \\ | ||
| + | -2 & 1 \\ | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|01c12NaUQDw|280|center|Inverse of Matrix}} | ||
==See Also== | ==See Also== | ||
| − | *[[Manuals/calci/ | + | *[[Manuals/calci/MMULT | MMULT ]] |
| − | *[[Manuals/calci/ | + | *[[Manuals/calci/MDETERM | MDETERM ]] |
| − | |||
| − | |||
==References== | ==References== | ||
| − | *[http://en.wikipedia.org/wiki/ | + | *[http://en.wikipedia.org/wiki/Invertible_matrix Matrix Inverse] |
| − | *[ | + | |
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 16:02, 24 July 2018
MINVERSE(a)
- is the array of numeric elements.
- MINVERSE(), returns the matrix inverse of an array.
Description
- This function gives the inverse matrix for the given matrix.
- We have to find a inverse of a matrix then it should satisfy the following conditions
- 1.A matrix must be a square matrix.
- 2.It's determinant not equal to 0.
- Let be the 2x2 matrix with the elements
.
- Then the inverse of matrix is denoted by .
- Now let be the matrix is of order .
- Then the inverse of is
- Where is the adjoint of .
- Adjoint is the matrix formed by taking the Transpose of the Co-factor matrix of the original matrix.
- Also , where is the identity matrix.
- Non-square matrices do not have inverses.
- Not all square matrices have inverses.
- A square matrix which has an inverse is called invertible or non-singular, and a square matrix without an inverse is called non-invertible or singular.
- This function will return the result as error when
1. Any one of the cell is non-numeric or any cell is empty or contain text 2. Suppose number of rows not equal to number of columns
ZOS
- The syntax is to calculate the inverse of the matrix in ZOS is .
- is the array of numeric elements.
- For e.g.,minverse([[10,12],[11,14]])
Examples
, because its determinant value is 0.
Related Videos
See Also
References
 is the array of numeric elements.
is the array of numeric elements.
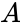 be the 2x2 matrix with the elements
be the 2x2 matrix with the elements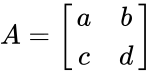 .
.
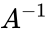 .
.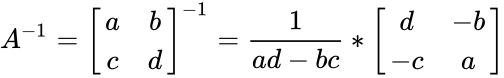
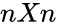 .
.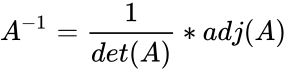
 is the adjoint of
is the adjoint of 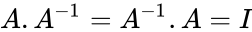 , where
, where 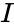 is the identity matrix.
is the identity matrix.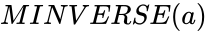 .
.
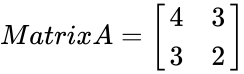
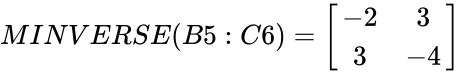
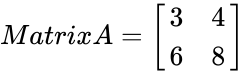
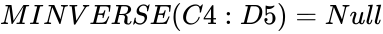 , because its determinant value is 0.
, because its determinant value is 0.