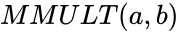Difference between revisions of "Manuals/calci/MMULT"
Jump to navigation
Jump to search
| (15 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''MMULT( | + | <div style="font-size:30px">'''MMULT(a,b)'''</div><br/> |
| − | *where <math> | + | *where <math>a</math> and <math>b</math> are the array of two matrices. |
| + | **MMULT(), returns the matrix product of two arrays. | ||
==Description== | ==Description== | ||
| Line 8: | Line 9: | ||
Type 2: Multiplication of two matrices. | Type 2: Multiplication of two matrices. | ||
*We can do the matrix multiplication when the number of columns in the first matrix equals the number of rows in the second matrix. | *We can do the matrix multiplication when the number of columns in the first matrix equals the number of rows in the second matrix. | ||
| − | *For e.g. 4x2 matrix can multiply with 2x3. The matrix product of two arrays <math>a</math> and <math>b</math> is <math> | + | *For e.g. 4x2 matrix can multiply with 2x3. The matrix product of two arrays <math>a</math> and <math>b</math> is: <math>x_{ij}= \sum_{k=1}^n a_{ik}.b_{kj}</math> where <math>i</math> is the row number and <math>j</math> is the column number. |
*i.e Multiply the elements of each row of 1st matrix by elements of each column of 2nd matrix. | *i.e Multiply the elements of each row of 1st matrix by elements of each column of 2nd matrix. | ||
*So the resultant matrix is of the order: Rows of 1st matrix × Columns of 2nd. | *So the resultant matrix is of the order: Rows of 1st matrix × Columns of 2nd. | ||
| − | *For e.g If we multiply a 4x2 matrix with a 2x3 matrix, the product matrix is of order 4x3 . | + | *For e.g If we multiply a 4x2 matrix with a 2x3 matrix, the product matrix is of order 4x3. |
| + | *Matrix multiplication satisfies the associative and distributive properties.But it is not satisfies the commutative property. | ||
| + | *i.e., Let A,B and C are three matrices, then A(BC)= (AB)C (Associative property) | ||
| + | *A(B+C)= AB+AC and (A+B)C = AC+BC (Distributive properties) | ||
| + | *k(AB)=(kA)B=A(kB)where k is a constant.But <math>AB \ne BA </math> (Commutative property) | ||
*This function will give the result as error when: | *This function will give the result as error when: | ||
The number of columns in the 1st matrix is not equal to number of rows in the 2nd matrix. | The number of columns in the 1st matrix is not equal to number of rows in the 2nd matrix. | ||
In the range cell, any cells are empty or that should not be convert in to numbers. | In the range cell, any cells are empty or that should not be convert in to numbers. | ||
| + | |||
| + | ==ZOS== | ||
| + | *The syntax is to calculate MMULT in ZOS is <math>MMULT(a,b)</math> | ||
| + | **where <math>a</math> and <math>b</math> are the array of two matrices. | ||
| + | *For e.g.,MMULT([[2.5,4,3,7],[1,3,5,4]],[[2,5,6],[7.3,4,9],[10,4,1],[6,2,8]]) | ||
| + | {{#ev:youtube|2lQ6XsvIbck|280|center|Matrix Multiplication}} | ||
==Examples== | ==Examples== | ||
| − | A | + | #'''Example 1''' |
| − | ''' | + | {| class="wikitable" |
| − | + | |+Spreadsheet | |
| + | |- | ||
| + | ! !! A !! B !! C !! D!! E | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 5 || 7 || 8 || || | ||
| + | |- | ||
| + | ! 2 | ||
| + | | 7 || 4 || || || | ||
| + | |- | ||
| + | ! 3 | ||
| + | | 8 || || || || | ||
| + | |- | ||
| + | ! 4 | ||
| + | | 4 ||-5 || 9 || || | ||
| + | |- | ||
| + | ! 5 | ||
| + | | || || || || | ||
| + | |} | ||
| + | '''From the above table values:''' | ||
| + | {| class="wikitable" | ||
| + | |+ =MMULT(3,A1:A3) | ||
| + | |- | ||
| + | | 15 | ||
| + | | 21 | ||
| + | | 24 | ||
| + | |} | ||
| + | {| class="wikitable" | ||
| + | |+=MMULT(6,A4:C4) | ||
| + | |- | ||
| + | | 24 | ||
| + | | -30 | ||
| + | | 54 | ||
| + | |} | ||
| − | {| class="wikitable" | + | #'''Example 2''' |
| − | |- | + | {| class="wikitable" |
| − | + | |+Matrix A | |
| − | + | |- | |
| − | + | | 7 || 5 | |
|- | |- | ||
| − | + | | 2 || 3 | |
| − | | | ||
| − | | | ||
|- | |- | ||
| − | + | | 6 || 0 | |
| − | | | ||
| − | | | ||
|- | |- | ||
| − | + | | 9 || 8 | |
| − | | | ||
| − | | | ||
|} | |} | ||
| − | * | + | {| class="wikitable" |
| − | * | + | |+Matrix B |
| − | + | |- | |
| − | + | | 8 || -4 ||11 | |
| + | |- | ||
| + | | 2 || 7 || 5 | ||
| + | |} | ||
| + | *Here Matrix A is of order 4x2 and Matrix B is of order 2x3. | ||
| + | *So the Product Matrix is of order 4x3. i.e | ||
| + | #'''1st Row''' 7*8+5*2 = 66 ; 7*(-4)+5*7 = 7 ; 7*11+5*5 = 102 | ||
| + | #'''2nd Row''' 2*8+3*2 = 22 ; 2*(-4)+3*7 = 13 ; 2*11+3*5 = 37 and so on | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|OMA2Mwo0aZg|280|center|Matrix Multiplication}} | ||
==See Also== | ==See Also== | ||
| Line 52: | Line 101: | ||
==References== | ==References== | ||
| − | [http://en.wikipedia.org/wiki/ | + | [http://en.wikipedia.org/wiki/Matrix_multiplication Matrix Multiplication] |
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 16:03, 24 July 2018
MMULT(a,b)
- where and are the array of two matrices.
- MMULT(), returns the matrix product of two arrays.
Description
- This function gives product of two matrices.
- Matrix multiplication is of two types:
Type 1: A scalar (a constant) is multiplied with the each element of the matrix. Type 2: Multiplication of two matrices.
- We can do the matrix multiplication when the number of columns in the first matrix equals the number of rows in the second matrix.
- For e.g. 4x2 matrix can multiply with 2x3. The matrix product of two arrays and is: where is the row number and is the column number.
- i.e Multiply the elements of each row of 1st matrix by elements of each column of 2nd matrix.
- So the resultant matrix is of the order: Rows of 1st matrix × Columns of 2nd.
- For e.g If we multiply a 4x2 matrix with a 2x3 matrix, the product matrix is of order 4x3.
- Matrix multiplication satisfies the associative and distributive properties.But it is not satisfies the commutative property.
- i.e., Let A,B and C are three matrices, then A(BC)= (AB)C (Associative property)
- A(B+C)= AB+AC and (A+B)C = AC+BC (Distributive properties)
- k(AB)=(kA)B=A(kB)where k is a constant.But (Commutative property)
- This function will give the result as error when:
The number of columns in the 1st matrix is not equal to number of rows in the 2nd matrix. In the range cell, any cells are empty or that should not be convert in to numbers.
ZOS
- The syntax is to calculate MMULT in ZOS is
- where and are the array of two matrices.
- For e.g.,MMULT([[2.5,4,3,7],[1,3,5,4]],[[2,5,6],[7.3,4,9],[10,4,1],[6,2,8]])
Examples
- Example 1
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | 5 | 7 | 8 | ||
| 2 | 7 | 4 | |||
| 3 | 8 | ||||
| 4 | 4 | -5 | 9 | ||
| 5 |
From the above table values:
| 15 | 21 | 24 |
| 24 | -30 | 54 |
- Example 2
| 7 | 5 |
| 2 | 3 |
| 6 | 0 |
| 9 | 8 |
| 8 | -4 | 11 |
| 2 | 7 | 5 |
- Here Matrix A is of order 4x2 and Matrix B is of order 2x3.
- So the Product Matrix is of order 4x3. i.e
- 1st Row 7*8+5*2 = 66 ; 7*(-4)+5*7 = 7 ; 7*11+5*5 = 102
- 2nd Row 2*8+3*2 = 22 ; 2*(-4)+3*7 = 13 ; 2*11+3*5 = 37 and so on
Related Videos
See Also
References
 and
and  are the array of two matrices.
are the array of two matrices.
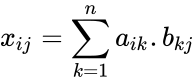 where
where  is the row number and
is the row number and  is the column number.
is the column number.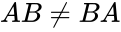 (Commutative property)
(Commutative property)