Difference between revisions of "Manuals/calci/INTERCEPT"
Jump to navigation
Jump to search
| (19 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''INTERCEPT( | + | <div style="font-size:30px">'''INTERCEPT (KnownYArray,KnownXArray)'''</div><br/> |
| − | *<math> | + | *<math>KnownYArray</math> is the set of dependent data |
| − | * <math> | + | *<math>KnownXArray</math> is the set of independent data. |
| + | **INTERCEPT(),returns the intercept of the linear regression line. | ||
==Description== | ==Description== | ||
| − | *This function is calculating the point where the line is | + | *This function is calculating the point where the line is intersecting y-axis using dependent and independent variables. |
*Using this function we can find the value of <math> y </math> when <math> x </math> is zero. | *Using this function we can find the value of <math> y </math> when <math> x </math> is zero. | ||
*The intercept point is finding using simple linear regression. | *The intercept point is finding using simple linear regression. | ||
| Line 10: | Line 11: | ||
*Regression methods nearly to the simple ordinary least squares also exist. | *Regression methods nearly to the simple ordinary least squares also exist. | ||
*i.e.,The Least Squares method relies on taking partial derivatives with respect to the slope and intercept which provides a solvable pair of equations called normal equations. | *i.e.,The Least Squares method relies on taking partial derivatives with respect to the slope and intercept which provides a solvable pair of equations called normal equations. | ||
| − | *Suppose there are <math> n </math> data points <math> {y_{i}, x_{i}}</math>, where i = 1, 2, | + | *Suppose there are <math> n </math> data points <math> {y_{i}, x_{i}}</math>, where <math>i = 1, 2,...n</math> |
*To find the equation of the regression line:<math> a=\bar{y}-b.\bar{x}</math>. | *To find the equation of the regression line:<math> a=\bar{y}-b.\bar{x}</math>. | ||
*This equation will give a "best" fit for the data points. | *This equation will give a "best" fit for the data points. | ||
| Line 16: | Line 17: | ||
*The slope is calculated by:<math> b=\frac{\sum_{i=1}^{n} {(x_{i}-\bar{x})(y_{i}-\bar{y})}} {\sum_{i=1}^{n}{(x_{i}-\bar{x})}^2}</math>. | *The slope is calculated by:<math> b=\frac{\sum_{i=1}^{n} {(x_{i}-\bar{x})(y_{i}-\bar{y})}} {\sum_{i=1}^{n}{(x_{i}-\bar{x})}^2}</math>. | ||
*In this formula<math> \bar{x}</math> and<math> \bar{y}</math> are the sample means AVERAGE of <math> x</math> and <math> y </math>. | *In this formula<math> \bar{x}</math> and<math> \bar{y}</math> are the sample means AVERAGE of <math> x</math> and <math> y </math>. | ||
| − | *In <math>INTERCEPT( | + | *In <math>INTERCEPT (KnownYArray,KnownXArray)</math>, the arguments can be numbers, names, arrays, or references that contain numbers. |
* The arrays values are disregarded when it is contains text, logical values or empty cells. | * The arrays values are disregarded when it is contains text, logical values or empty cells. | ||
| − | *This function will return the result as error when any one of the argument is | + | *This function will return the result as error when any one of the argument is non-numeric or <math>x</math> and <math>y</math> is having different number of data points and there is no data. |
| − | |||
| − | + | ==ZOS== | |
| + | *The syntax is to calculate intercept of the regression line in ZOS is <math>INTERCEPT (KnownYArray,KnownXArray)</math>. | ||
| + | **<math>KnownYArray</math> is the set of dependent data | ||
| + | **<math>KnownXArray</math> is the set of independent data. | ||
| + | *For e.g.,intercept([14,16,19,15.25],[20.1,26,10,26.4]) | ||
| + | {{#ev:youtube|ltc2nl-pwpk|280|center|Intercept}} | ||
| − | + | ==Examples== | |
| + | {| class="wikitable" | ||
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! !! A !! B !! C !! D!! E | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 4 || 5 || 2 ||10 || | ||
| + | |- | ||
| + | ! 2 | ||
| + | | 12 || 20 || 15 || 11 || | ||
| + | |- | ||
| + | ! 3 | ||
| + | | 25 || -12 || -9 ||30 ||18 | ||
| + | |- | ||
| + | ! 4 | ||
| + | | 10 ||15 || -40 ||52 ||36 | ||
| + | |} | ||
| − | + | #=INTERCEPT(A1:D1,A2:D2)= 10.13265306 | |
| − | + | #=INTERCEPT(A3:E3,A4:E4)= 4.754939085 | |
| − | |||
| − | + | ==Related Videos== | |
| − | + | {{#ev:youtube|LNSB0N6esPU|280|center|INTERCEPTS}} | |
| − | |||
| − | |||
| − | + | ==See Also== | |
| + | *[[Manuals/calci/PEARSON | PEARSON ]] | ||
| + | *[[Manuals/calci/AVERAGE | AVERAGE ]] | ||
| − | + | ==References== | |
| + | *[http://www.purplemath.com/modules/intrcept.htm INTERCEPT] | ||
| − | |||
| − | |||
| − | + | *[[Z_API_Functions | List of Main Z Functions]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *[[ Z3 | Z3 home ]] | |
| − | |||
Latest revision as of 16:04, 1 August 2018
INTERCEPT (KnownYArray,KnownXArray)
- is the set of dependent data
- is the set of independent data.
- INTERCEPT(),returns the intercept of the linear regression line.
Description
- This function is calculating the point where the line is intersecting y-axis using dependent and independent variables.
- Using this function we can find the value of when is zero.
- The intercept point is finding using simple linear regression.
- It is fits a straight line through the set of points in such a way that makes vertical distances between the points of the data set and the fitted line as small as possible.
- Regression methods nearly to the simple ordinary least squares also exist.
- i.e.,The Least Squares method relies on taking partial derivatives with respect to the slope and intercept which provides a solvable pair of equations called normal equations.
- Suppose there are data points , where
- To find the equation of the regression line:.
- This equation will give a "best" fit for the data points.
- The "best" means least-squares method. Here b is the slope.
- The slope is calculated by:.
- In this formula and are the sample means AVERAGE of and .
- In , the arguments can be numbers, names, arrays, or references that contain numbers.
- The arrays values are disregarded when it is contains text, logical values or empty cells.
- This function will return the result as error when any one of the argument is non-numeric or and is having different number of data points and there is no data.
ZOS
- The syntax is to calculate intercept of the regression line in ZOS is .
- is the set of dependent data
- is the set of independent data.
- For e.g.,intercept([14,16,19,15.25],[20.1,26,10,26.4])
Examples
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | 4 | 5 | 2 | 10 | |
| 2 | 12 | 20 | 15 | 11 | |
| 3 | 25 | -12 | -9 | 30 | 18 |
| 4 | 10 | 15 | -40 | 52 | 36 |
- =INTERCEPT(A1:D1,A2:D2)= 10.13265306
- =INTERCEPT(A3:E3,A4:E4)= 4.754939085
Related Videos
See Also
References
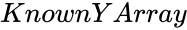 is the set of dependent data
is the set of dependent data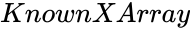 is the set of independent data.
is the set of independent data.
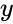 when
when  is zero.
is zero. points in such a way that makes vertical distances between the points of the data set and the fitted line as small as possible.
points in such a way that makes vertical distances between the points of the data set and the fitted line as small as possible.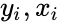 , where
, where 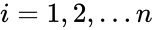
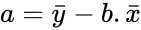 .
.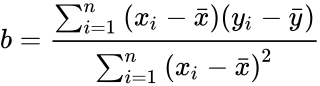 .
.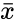 and
and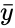 are the sample means AVERAGE of
are the sample means AVERAGE of 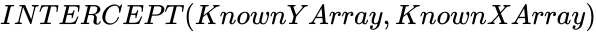 , the arguments can be numbers, names, arrays, or references that contain numbers.
, the arguments can be numbers, names, arrays, or references that contain numbers.