Difference between revisions of "Manuals/calci/SLOPE"
Jump to navigation
Jump to search
| (14 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''SLOPE( | + | <div style="font-size:30px">'''SLOPE (KnownYArray,KnownXArray)'''</div><br/> |
| − | *<math> | + | *<math> KnownYArray </math> is the set of dependent values. |
| − | *<math> | + | *<math> KnownXArray </math> is the set of independent values. |
| − | + | **SLOPE(), returns the slope of the linear regression line. | |
==Description== | ==Description== | ||
*This function gives the slope of the linear regression line through a set of given points. | *This function gives the slope of the linear regression line through a set of given points. | ||
| − | *The slope of a regression line (b) represents the rate of change in y as x changes. | + | *The slope of a regression line (b) represents the rate of change in <math> y </math> as ,math> x </math> changes. |
*To find a slope we can use the least squares method. | *To find a slope we can use the least squares method. | ||
| − | *Slope is found by calculating b as the | + | *Slope is found by calculating b as the co-variance of <math>x</math> and <math>y</math>, divided by the sum of squares (variance) of <math>x</math>. |
| − | *In SLOPE( | + | *In <math>SLOPE (KnownYArray,KnownXArray)</math>, <math>KnownYArray </math> is the array of the numeric dependent values and <math> KnownXArray </math> is the array of the independent values. |
| − | *The arguments can be be either numbers or names, array,constants or references that contain numbers. | + | *The arguments can be be either numbers or names, array, constants or references that contain numbers. |
| − | *Suppose the array contains text,logical values or empty cells, like that values are not considered. | + | *Suppose the array contains text, logical values or empty cells, like that values are not considered. |
| − | *The equation for the slope of the regression line is :<math>b = \frac {\sum (x-\bar{x})(y-\bar{y})} {\sum(x-\bar{x})^2</math> | + | *The equation for the slope of the regression line is |
| + | :<math>b = \frac {\sum (x-\bar{x})(y-\bar{y})} {\sum(x-\bar{x})^2}</math> | ||
| + | where <math>\bar{x}</math> and <math>\bar{y}</math> are the sample mean x and y. | ||
*This function will return the result as error when | *This function will return the result as error when | ||
| − | 1. Any one of the argument is | + | 1. Any one of the argument is non-numeric. |
| − | 2. | + | 2. <math>KnownYArray</math> and <math>KnownXArray</math> are empty or that have a different number of data points. |
==Examples== | ==Examples== | ||
| − | 1. | + | 1. |
| − | + | {| class="wikitable" | |
| − | SLOPE(A1: | + | |+Spreadsheet |
| − | 2. | + | |- |
| − | + | ! !! A !! B !! C !! D!! E | |
| − | + | |- | |
| − | + | ! 1 | |
| − | + | | 4 || 9 || 2 ||6 || 7 | |
| − | + | |- | |
| + | ! 2 | ||
| + | | 1 || 5 || 10 || 3 || 4 | ||
| + | |} | ||
| + | =SLOPE(A1:E1,A2:E2) = -0.305309734513 | ||
| + | 2. | ||
| + | {| class="wikitable" | ||
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! !! A !! B !! C !! D!! E !!F | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 2 || 9 || 3 ||8 || 10 ||17 | ||
| + | |- | ||
| + | ! 2 | ||
| + | | 4 || 5 || 11 || 7 || 15 ||12 | ||
| + | |} | ||
| + | =SLOPE(A1:F1,A2:F2) = 0.58510638297 | ||
| + | |||
| + | 3. | ||
| + | {| class="wikitable" | ||
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! !! A !! B !! C | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 0 || 9 || 4 | ||
| + | |- | ||
| + | ! 2 | ||
| + | | -1 || 5 || 7 | ||
| + | |} | ||
| + | =SLOPE(C1:C3) = 0.730769230769 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|MeU-KzdCBps|280|center|SLOPE}} | ||
==See Also== | ==See Also== | ||
| Line 34: | Line 71: | ||
*[[Manuals/calci/PEARSON | PEARSON ]] | *[[Manuals/calci/PEARSON | PEARSON ]] | ||
| + | ==References== | ||
| + | *[http://stattrek.com/regression/slope-test.aspx?Tutorial=AP Linear regression line] | ||
| − | + | ||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 16:12, 1 August 2018
SLOPE (KnownYArray,KnownXArray)
- is the set of dependent values.
- is the set of independent values.
- SLOPE(), returns the slope of the linear regression line.
Description
- This function gives the slope of the linear regression line through a set of given points.
- The slope of a regression line (b) represents the rate of change in as ,math> x </math> changes.
- To find a slope we can use the least squares method.
- Slope is found by calculating b as the co-variance of and , divided by the sum of squares (variance) of .
- In , is the array of the numeric dependent values and is the array of the independent values.
- The arguments can be be either numbers or names, array, constants or references that contain numbers.
- Suppose the array contains text, logical values or empty cells, like that values are not considered.
- The equation for the slope of the regression line is
where and are the sample mean x and y.
- This function will return the result as error when
1. Any one of the argument is non-numeric. 2. and are empty or that have a different number of data points.
Examples
1.
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | 4 | 9 | 2 | 6 | 7 |
| 2 | 1 | 5 | 10 | 3 | 4 |
=SLOPE(A1:E1,A2:E2) = -0.305309734513
2.
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | 2 | 9 | 3 | 8 | 10 | 17 |
| 2 | 4 | 5 | 11 | 7 | 15 | 12 |
=SLOPE(A1:F1,A2:F2) = 0.58510638297
3.
| A | B | C | |
|---|---|---|---|
| 1 | 0 | 9 | 4 |
| 2 | -1 | 5 | 7 |
=SLOPE(C1:C3) = 0.730769230769
Related Videos
See Also
References
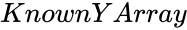 is the set of dependent values.
is the set of dependent values.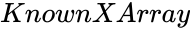 is the set of independent values.
is the set of independent values.
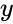 as ,math> x </math> changes.
as ,math> x </math> changes. and
and 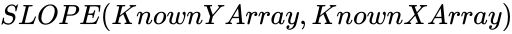 ,
, 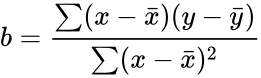
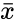 and
and 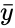 are the sample mean x and y.
are the sample mean x and y.