Difference between revisions of "Manuals/calci/FTEST"
Jump to navigation
Jump to search
| (13 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''FTEST( | + | <div style="font-size:30px">'''FTEST(Array1,Array2)'''</div><br/> |
| − | *<math> | + | *<math>Array1</math> and <math>Array2 </math> are array of data. |
| + | **FTEST(), returns the result of an F-test. | ||
| + | |||
==Description== | ==Description== | ||
*This function gives the result of F-test. | *This function gives the result of F-test. | ||
| Line 6: | Line 8: | ||
*It does this by comparing the ratio of two variances. | *It does this by comparing the ratio of two variances. | ||
*So, if the variances are equal, the ratio of the variances will be 1. | *So, if the variances are equal, the ratio of the variances will be 1. | ||
| − | *Let X1,...Xn and Y1...Ym be independent samples each have a Normal Distribution . | + | *Let X1,...Xn and Y1,...Ym be independent samples each have a Normal Distribution . |
*It's sample means: | *It's sample means: | ||
<math>\bar X=\frac{1}{n} \sum_{i=1}^n Xi</math> | <math>\bar X=\frac{1}{n} \sum_{i=1}^n Xi</math> | ||
| Line 15: | Line 17: | ||
and | and | ||
:<math>SY^2=\frac{1}{m-1} \sum_{i=1}^m (Yi-\bar Y)^2</math> | :<math>SY^2=\frac{1}{m-1} \sum_{i=1}^m (Yi-\bar Y)^2</math> | ||
| − | *Then the Test Statistic = <math>\frac {Sx^2}{Sy^2}</math> has an F-distribution with | + | *Then the Test Statistic = <math>\frac {Sx^2}{Sy^2}</math> has an F-distribution with 'n−1' and 'm−1' degrees of freedom. |
| − | *In FTEST( | + | *In FTEST(Array1,Array2) where <math>Array1</math> is the data of first array, <math>Array2</math> is the data of second array. |
*The array may be any numbers, names, or references that contains numbers. | *The array may be any numbers, names, or references that contains numbers. | ||
*values are not considered if the array contains any text, logical values or empty cells. | *values are not considered if the array contains any text, logical values or empty cells. | ||
| − | When the <math> | + | When the <math>Array1</math> or <math>Array2</math> is less than 2 or the variance of the array value is zero, then this function will return the result as error. |
| + | |||
| + | ==ZOS== | ||
| + | *The syntax is to calculate FTEST in ZOS is <math>FTEST(Array1,Array2)</math>. | ||
| + | **<math>Array1</math> and <math>Array2 </math> are array of data. | ||
| + | *For e.g.,FTEST([15,29,30],[62,74,80]) | ||
| + | {{#ev:youtube|y_uVl6UbHtE|280|center|F-Test}} | ||
==Examples== | ==Examples== | ||
| Line 96: | Line 104: | ||
|} | |} | ||
=FTEST(B1,C2:C3)=NAN | =FTEST(B1,C2:C3)=NAN | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|tscL1fzjSTY|280|center|F-Test}} | ||
==See Also== | ==See Also== | ||
*[[Manuals/calci/FDIST | FDIST ]] | *[[Manuals/calci/FDIST | FDIST ]] | ||
*[[Manuals/calci/FINV | FINV ]] | *[[Manuals/calci/FINV | FINV ]] | ||
| − | |||
==References== | ==References== | ||
[http://en.wikipedia.org/wiki/F-test F Test] | [http://en.wikipedia.org/wiki/F-test F Test] | ||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 16:07, 7 August 2018
FTEST(Array1,Array2)
- and are array of data.
- FTEST(), returns the result of an F-test.
Description
- This function gives the result of F-test.
- The F-test is designed to test if two population variances are equal.
- It does this by comparing the ratio of two variances.
- So, if the variances are equal, the ratio of the variances will be 1.
- Let X1,...Xn and Y1,...Ym be independent samples each have a Normal Distribution .
- It's sample means:
and
- .
- The sample variances :
and
- Then the Test Statistic = has an F-distribution with 'n−1' and 'm−1' degrees of freedom.
- In FTEST(Array1,Array2) where is the data of first array, is the data of second array.
- The array may be any numbers, names, or references that contains numbers.
- values are not considered if the array contains any text, logical values or empty cells.
When the or is less than 2 or the variance of the array value is zero, then this function will return the result as error.
ZOS
- The syntax is to calculate FTEST in ZOS is .
- and are array of data.
- For e.g.,FTEST([15,29,30],[62,74,80])
Examples
1.
| 15 | 27 | 19 | 32 |
| 21 | 12 | 30 | 11 |
=FTEST(B4:B8,C4:C8)=0.81524906747183
2.
| 5 | 8 | 12 | 45 | 23 |
| 10 | 20 | 30 | 40 | 50 |
=FTEST(A1:A5,C1:C5)=0.9583035732212274
3.
| 14 | 26 | 37 |
| 45 | 82 | 21 | 17 |
FTEST(B1:B3,C1:C4} = 0.26412211240525474
4.
| 14 |
| 45 | 65 |
=FTEST(B1,C2:C3)=NAN
Related Videos
See Also
References
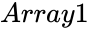 and
and 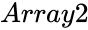 are array of data.
are array of data.
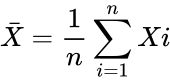 and
and
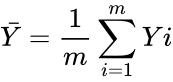 .
.
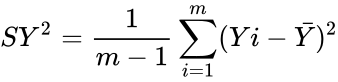
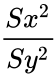 has an F-distribution with 'n−1' and 'm−1' degrees of freedom.
has an F-distribution with 'n−1' and 'm−1' degrees of freedom.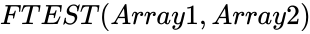 .
.