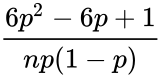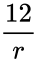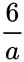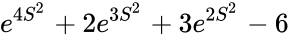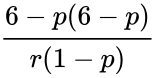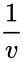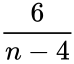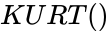Difference between revisions of "Manuals/calci/KURT"
Jump to navigation
Jump to search
| (13 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''KURT( | + | <div style="font-size:30px">'''KURT()'''</div><br/> |
| − | * | + | *Parameters are any values to calculate kurtosis. |
| + | **KURT(), returns the kurtosis of a data set. | ||
| + | |||
==Description== | ==Description== | ||
*This function gives the value of Kurtosis of a given set. | *This function gives the value of Kurtosis of a given set. | ||
| Line 20: | Line 22: | ||
3.The referred arguments could not convert | 3.The referred arguments could not convert | ||
in to numbers. | in to numbers. | ||
| + | * When calculating kurtosis, a result of +3.00 indicates the absence of kurtosis (distribution is mesokurtic). | ||
| + | *For simplicity in its interpretation, some statisticians adjust this result to zero (i.e. kurtosis minus 3 equals zero), and then any reading other than zero is referred to as excess kurtosis. | ||
| + | *Negative numbers indicate a platykurtic distribution and positive numbers indicate a leptokurtic distribution. | ||
*The below table is listing the Kurtosis excess for the number of common distributions: | *The below table is listing the Kurtosis excess for the number of common distributions: | ||
{| class="wikitable" | {| class="wikitable" | ||
| Line 37: | Line 42: | ||
| Gamma distribution || <math> \frac {6}{a}</math> | | Gamma distribution || <math> \frac {6}{a}</math> | ||
|- | |- | ||
| − | |Log normal distribution ||<math>e^{4S^2}+2e^{3S^2}+3e^{2S^2}-6</math> | + | | Log normal distribution ||<math>e^{4S^2}+2e^{3S^2}+3e^{2S^2}-6</math> |
| + | |- | ||
| + | | Negative binomial distribution ||<math>\frac{6-p(6-p)}{r(1-p)}</math> | ||
| + | |- | ||
| + | | Normal distribution || 0 | ||
| + | |- | ||
| + | | Poisson distribution || <math>\frac{1}{v}</math> | ||
| + | |- | ||
| + | | Student's t distribution ||<math>\frac{6}{n-4}</math> | ||
|} | |} | ||
| + | |||
| + | ==ZOS== | ||
| + | *The syntax is to calculate KURTOSIS in ZOS is <math>KURT()</math> | ||
| + | **Parameters are any values to calculate kurtosis. | ||
| + | *For e.g., KURT([-1..-10,20..25..0.5]) | ||
| + | {{#ev:youtube|YqusfrKpWEA|280|center|KURTOSIS}} | ||
==Examples== | ==Examples== | ||
| Line 47: | Line 66: | ||
|- | |- | ||
! 1 | ! 1 | ||
| − | | 14 || 11 || 23 ||54||38 | + | | 14 || 11 || 23 || 54 || 38 |
|- | |- | ||
! 2 | ! 2 | ||
| Line 57: | Line 76: | ||
! 4 | ! 4 | ||
| 26 ||16 || 12 || || | | 26 ||16 || 12 || || | ||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| − | # =KURT(A1:E1) = 0. | + | # =KURT(A1:E1) = -0.8704870491886512 |
# =KURT(A2:E2) = -1.199999999 | # =KURT(A2:E2) = -1.199999999 | ||
| − | # =KURT(A3:D3) = 0. | + | # =KURT(A3:D3) = 0.8709011137293157 |
# =KURT(A4:C4) = NAN | # =KURT(A4:C4) = NAN | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|HnMGKsupF8Q|280|center|Kurtosis}} | ||
==See Also== | ==See Also== | ||
| Line 73: | Line 93: | ||
==References== | ==References== | ||
[http://en.wikipedia.org/wiki/Kurtosis Kurtosis] | [http://en.wikipedia.org/wiki/Kurtosis Kurtosis] | ||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 16:22, 7 August 2018
KURT()
- Parameters are any values to calculate kurtosis.
- KURT(), returns the kurtosis of a data set.
Description
- This function gives the value of Kurtosis of a given set.
- Kurtosis is the peak or flatness of a frequency distribution graph especially with respect to the concentration of values near the Mean as compared with the Normal Distribution.
- A normal distribution has a Kurtosis of 3.
- Distributions having higher Kurtosis have flatter tails or more extreme values that phenomenon called 'leptokurtosis' also it is the positive excess Kurtosis , and those with lower Kurtosis have fatter middles or fewer extreme value that phenomenon called 'Platykurtosis' also it is the negative excess Kurtosis.
- Example for positive Kurtosis(leptokurtosis) is Exponential distribution, Poisson distribution, Laplace Distribution.
- Example for Negative Kurtosis(platykurtosis) is Bernoulli distribution, Uniform distribution.
- Kurtosis has no units.
- Kurtosis is defined by:
- Kurtosis=:
, where is the Sample Standard Deviation. is the Arithmetic Mean.
- In this function arguments may be any type like numbers,names,arrays or references that contain numbers.
- We can give logical values and text references also directly.
- Suppose the referred argument contains any null cells, logical values like that values are not considered.
- This function will return the result as error when
1.Any one of the argument is non-numeric. 2.Suppose the number of data points are less than four or the standard deviation of the sample is zero 3.The referred arguments could not convert in to numbers.
- When calculating kurtosis, a result of +3.00 indicates the absence of kurtosis (distribution is mesokurtic).
- For simplicity in its interpretation, some statisticians adjust this result to zero (i.e. kurtosis minus 3 equals zero), and then any reading other than zero is referred to as excess kurtosis.
- Negative numbers indicate a platykurtic distribution and positive numbers indicate a leptokurtic distribution.
- The below table is listing the Kurtosis excess for the number of common distributions:
| Distribution | Kurtosis excess |
|---|---|
| Bernoulli distribution | |
| Beta distribution | |
| Binomial distribution | |
| Chi squared distribution | |
| Exponential distribution | 6 |
| Gamma distribution | |
| Log normal distribution | |
| Negative binomial distribution | |
| Normal distribution | 0 |
| Poisson distribution | |
| Student's t distribution |
ZOS
- The syntax is to calculate KURTOSIS in ZOS is
- Parameters are any values to calculate kurtosis.
- For e.g., KURT([-1..-10,20..25..0.5])
Examples
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | 14 | 11 | 23 | 54 | 38 |
| 2 | 6 | 7 | 8 | 9 | 10 |
| 3 | 1898 | 1987 | 1786 | 1947 | |
| 4 | 26 | 16 | 12 |
- =KURT(A1:E1) = -0.8704870491886512
- =KURT(A2:E2) = -1.199999999
- =KURT(A3:D3) = 0.8709011137293157
- =KURT(A4:C4) = NAN
Related Videos
See Also
References
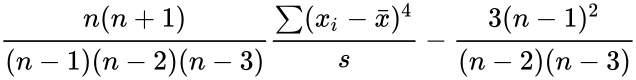 , where
, where 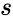 is the Sample Standard Deviation.
is the Sample Standard Deviation.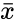 is the Arithmetic Mean.
is the Arithmetic Mean.
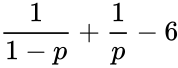
![{\displaystyle {\frac {6[a^{3}+a^{2}(1-2b)+b^{2}(1+b)-2ab(2+b)]}{ab(2+a+b)(3+a+b)}}}](https://wikimedia.org/api/rest_v1/media/math/render/png/e455ad035a71ee4a59d2f442314f6c7606293790)