Difference between revisions of "Manuals/calci/NEGBINOMDIST"
Jump to navigation
Jump to search
| (3 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
*<math>r</math> is the number of successes on an individual trial | *<math>r</math> is the number of successes on an individual trial | ||
*<math>p</math> is the probability of a success. | *<math>p</math> is the probability of a success. | ||
| + | **NEGBINOMDIST(), returns the negative binomial distribution. | ||
==Description== | ==Description== | ||
| Line 26: | Line 27: | ||
#If <math>nf<0</math> or <math>ns<1</math> | #If <math>nf<0</math> or <math>ns<1</math> | ||
| − | ==ZOS | + | ==ZOS== |
*The syntax is to calculate NEGBINOMDIST in ZOS is <math>NEGBINOMDIST(x,r,p)</math>. | *The syntax is to calculate NEGBINOMDIST in ZOS is <math>NEGBINOMDIST(x,r,p)</math>. | ||
**where <math>x</math> is the number of failures. | **where <math>x</math> is the number of failures. | ||
| Line 58: | Line 59: | ||
==References== | ==References== | ||
[http://en.wikipedia.org/wiki/Logarithm Logarithm] | [http://en.wikipedia.org/wiki/Logarithm Logarithm] | ||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 14:58, 8 August 2018
NEGBINOMDIST(x,r,p)
- is the number of failures.
- is the number of successes on an individual trial
- is the probability of a success.
- NEGBINOMDIST(), returns the negative binomial distribution.
Description
- This function gives the Negative Binomial Distribution.
- Negative Binomial Distribution is the discrete probability distribution with the fixed probability of success.
- It is also called Pascal Distribution.
This is the statistical experiment with the following conditions:
This experiment consists of a sequence of independent trials. Each trial represents only two results(Success or failure) The probability of success is constant from trial to trial The trials are independent; ie, the outcome on one trial does not affect the outcome on other trials. The experiment continues until the successes is obtained, where is a specified positive integer.
- The random variable = the number of failures that precede the success;
- is called a Negative Binomial Random variable because, in contrast to the
binomial random variable, the number of successes is fixed and the number of trials is random.
- Then probability mass function of the negative binomial distribution is
- For example: If a fair coin is tossed repeatedly, what is the probability that at least 10 tosses are required.
to obtain heads 8 times
- This function will give the result as error when:
- Any argument is non-numeric
- If or
- If or
ZOS
- The syntax is to calculate NEGBINOMDIST in ZOS is .
- where is the number of failures.
- is the number of successes on an individual trial
- is the probability of a success.
- For e.g.,NEGBINOMDIST(8..9,5..7,0.5).
Examples
- Find the probability that a man flipping a coin gets the fourth head on the ninth flip.
Here total number of events =9, r= 4(since we define Heads as a success) and x=9-4=5(number of failures)
p=1/2=0.5(Probability of success for any coin flip)
NEGBINOMDIST(5,4,0.5)=0.109375
- A company conducts a geological study that indicates that an exploratory goods well should have a 20% chance of striking goods. What is the probability that the first strike comes on the third well drilled?
Here total number of events=3, r=1,x=3-1=2,and p=0.20 NEGBINOMDIST(2,1,0.20)=0.128
- What is the probability that the fourth strike comes on the eighth well drilled?
Here total number of events=8, r=4, x=8-4=4 and p=0.20 NEGBINOMDIST(4,4,0.20)=0.0229376
Related Videos
See Also
References
 is the number of failures.
is the number of failures.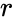 is the number of successes on an individual trial
is the number of successes on an individual trial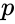 is the probability of a success.
is the probability of a success.
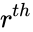 success;
success;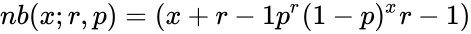
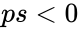 or
or 
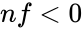 or
or 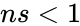
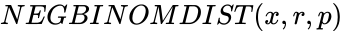 .
.