Difference between revisions of "Manuals/calci/PEARSON"
Jump to navigation
Jump to search
| (12 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''PEARSON ( | + | <div style="font-size:30px">'''PEARSON (Array1,Array2)'''</div><br/> |
| − | *<math> | + | *<math>Array1</math> is the array of independent values |
| + | *<math>Array2</math> is the array of dependent values. | ||
| + | **PEARSON(),returns the Pearson product moment correlation coefficient. | ||
==Description== | ==Description== | ||
| − | *This function gives the Pearson | + | *This function gives the Pearson Product-Moment Correlation Coefficient. |
*It is denoted by PPMC, which shows the linear relationship between two variables. | *It is denoted by PPMC, which shows the linear relationship between two variables. | ||
*It is a measure of the strength of a linear association between two variables . | *It is a measure of the strength of a linear association between two variables . | ||
| − | *The two variables X and Y, giving a value between +1 and −1 inclusive. | + | *The two variables <math> X </math> and <math> Y </math>, giving a value between +1 and −1 inclusive. |
| − | *Here +1 indicates the perfect positive correlation, 0 indicates no correlation | + | *Here |
| − | *The formula for PPMC,r is defined by: | + | +1 indicates the perfect positive correlation, |
| + | 0 indicates no correlation | ||
| + | -1 indicates the perfect negative correlation. | ||
| + | *The formula for PPMC, <math> r </math> is defined by: | ||
<math> r= \frac{ \Sigma(x-\bar{x})(y-\bar{y})}{\sqrt {\Sigma(x-\bar{x})^2(y-\bar{y})^2}}</math> | <math> r= \frac{ \Sigma(x-\bar{x})(y-\bar{y})}{\sqrt {\Sigma(x-\bar{x})^2(y-\bar{y})^2}}</math> | ||
| − | where <math>\bar{x} and \bar{y} </math> are Average of the two Samples x and y. | + | where <math> \bar{x}</math> and <math>\bar{y} </math> are Average of the two Samples <math>x </math> and <math>y </math>. |
| − | *In <math>PEARSON( | + | *In <math>PEARSON(Array1,Array2)</math>, the value of <math>Array1</math> and <math>Array2</math> must be either numbers or names, array,constants or references that contain numbers. |
| − | *Suppose the array contains text,logicl values or empty cells, like that values are not considered. | + | *Suppose the array contains text, logicl values or empty cells, like that values are not considered. |
| − | *This function will return the result as error when the number of values are different for | + | *This function will return the result as error when the number of values are different for <math> Array1 </math> and <math> Array2 </math>. |
==Examples== | ==Examples== | ||
| − | + | {| class="wikitable" | |
| − | + | |+Spreadsheet | |
| − | + | |- | |
| − | + | ! !! A !! B !! C | |
| − | + | |- | |
| − | + | ! 1 | |
| − | + | | 5 || 9 || 10 | |
| − | + | |- | |
| − | + | ! 2 | |
| − | + | | 8 || 12 || 15 | |
| − | + | |} | |
| − | |||
| − | |||
| − | 2 | ||
| − | |||
| − | |||
| + | =PEARSON(A1:C1,A2:C2) = 0.968619605 | ||
| + | 2. | ||
| + | {| class="wikitable" | ||
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! !! A !! B !! C !!D | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 17 || 0 || 19 ||25 | ||
| + | |- | ||
| + | ! 2 | ||
| + | | 10 || 11 || 7 ||13 | ||
| + | |} | ||
| + | |||
| + | =PEARSON(A1:D1,A2:D2) = 0.034204238054579846 | ||
| + | |||
| + | 3. | ||
| + | {| class="wikitable" | ||
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! !! A !! B !! C | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 1 || 2 || 3 | ||
| + | |- | ||
| + | ! 2 | ||
| + | | 4 || 5 || | ||
| + | |} | ||
| + | |||
| + | =PEARSON(A1:C1,A2:B2) = NAN | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|JO-Gc5bEG70|280|center|PEARSON}} | ||
==See Also== | ==See Also== | ||
| Line 40: | Line 74: | ||
==References== | ==References== | ||
| + | [http://en.wikipedia.org/wiki/Pearson_product-moment_correlation_coefficient Pearson] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 15:01, 8 August 2018
PEARSON (Array1,Array2)
- is the array of independent values
- is the array of dependent values.
- PEARSON(),returns the Pearson product moment correlation coefficient.
Description
- This function gives the Pearson Product-Moment Correlation Coefficient.
- It is denoted by PPMC, which shows the linear relationship between two variables.
- It is a measure of the strength of a linear association between two variables .
- The two variables and , giving a value between +1 and −1 inclusive.
- Here
+1 indicates the perfect positive correlation, 0 indicates no correlation -1 indicates the perfect negative correlation.
- The formula for PPMC, is defined by:
where and are Average of the two Samples and .
- In , the value of and must be either numbers or names, array,constants or references that contain numbers.
- Suppose the array contains text, logicl values or empty cells, like that values are not considered.
- This function will return the result as error when the number of values are different for and .
Examples
| A | B | C | |
|---|---|---|---|
| 1 | 5 | 9 | 10 |
| 2 | 8 | 12 | 15 |
=PEARSON(A1:C1,A2:C2) = 0.968619605
2.
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 17 | 0 | 19 | 25 |
| 2 | 10 | 11 | 7 | 13 |
=PEARSON(A1:D1,A2:D2) = 0.034204238054579846
3.
| A | B | C | |
|---|---|---|---|
| 1 | 1 | 2 | 3 |
| 2 | 4 | 5 |
=PEARSON(A1:C1,A2:B2) = NAN
Related Videos
See Also
References
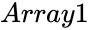 is the array of independent values
is the array of independent values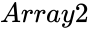 is the array of dependent values.
is the array of dependent values.
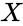 and
and 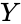 , giving a value between +1 and −1 inclusive.
, giving a value between +1 and −1 inclusive.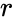 is defined by:
is defined by:
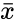 and
and 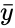 are Average of the two Samples
are Average of the two Samples  and
and 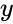 .
.
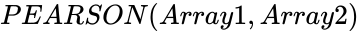 , the value of
, the value of