Difference between revisions of "Manuals/calci/PERCENTILE"
Jump to navigation
Jump to search
| (7 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">''' PERCENTILE( | + | <div style="font-size:30px">''' PERCENTILE (Array,kth) '''</div><br/> |
| − | *<math> | + | *<math>Array</math> is the array of data . |
| − | *<math> | + | *<math>kth </math> is the Percentile value. |
| + | **PERCENTILE(),returns the k-th percentile of values in a range. | ||
==Description== | ==Description== | ||
| Line 7: | Line 8: | ||
*Percentile means any of the 100 equal parts into which the range of the values of a set of data can be divided in order to show the distribution of those values. | *Percentile means any of the 100 equal parts into which the range of the values of a set of data can be divided in order to show the distribution of those values. | ||
*The percentile of a given value is determined by the percentage of the values that are smaller than that value. | *The percentile of a given value is determined by the percentage of the values that are smaller than that value. | ||
| − | *For example we can have the <math>25^th</math> percentile is the value below which 25 percent of the observations may be found. | + | *For example we can have the <math>25^{th}</math> percentile is the value below which 25 percent of the observations may be found. |
*The 25th percentile is called as the first quartile (Q1), the 50th percentile as the median quartile (Q2), and the 75th percentile as the third quartile (Q3). | *The 25th percentile is called as the first quartile (Q1), the 50th percentile as the median quartile (Q2), and the 75th percentile as the third quartile (Q3). | ||
*In general, percentiles and quartiles are specific types of quantiles. | *In general, percentiles and quartiles are specific types of quantiles. | ||
| − | *In <math>PERCENTILE( | + | *In <math>PERCENTILE(Array,kth)</math>, <math>Array</math> is the array of data that indicating relative standing and <math>kth </math> is the Percentile value in the range <math>0...1</math>(inclusive). |
*This function will return the result as error when | *This function will return the result as error when | ||
1. The array value is empty. | 1. The array value is empty. | ||
| Line 16: | Line 17: | ||
==Examples== | ==Examples== | ||
| − | + | 1. | |
| − | 7 | + | {| class="wikitable" |
| − | 2 | + | |+Spreadsheet |
| − | + | |- | |
| − | PERCENTILE( | + | ! !! A !! B !! C !! D |
| − | + | |- | |
| − | 20 | + | ! 1 |
| − | 12 | + | | 5 || 7 || 2 || 9 |
| − | 41 | + | |} |
| − | + | =PERCENTILE(A1:D1,0.4) = 5.4 | |
| − | PERCENTILE( | + | 2. |
| − | + | {| class="wikitable" | |
| − | 3 | + | |+Spreadsheet |
| − | 4 | + | |- |
| − | PERCENTILE(A1:A3,1.1)=NAN | + | ! !! A !! B !! C !! D !! E |
| + | |- | ||
| + | ! 1 | ||
| + | | 15 || 20 || 12 || 41 ||35 | ||
| + | |} | ||
| + | =PERCENTILE(A1:E1,0.721) = 33.26 | ||
| + | |||
| + | 3. | ||
| + | {| class="wikitable" | ||
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! !! A !! B !! C | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 2 || 3 || 4 | ||
| + | |} | ||
| + | =PERCENTILE(A1:A3,1.1) = NAN | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|g76wlb_7HSk|280|center|PERCENTILE}} | ||
==See Also== | ==See Also== | ||
| Line 41: | Line 62: | ||
* [http://en.wikipedia.org/wiki/Percentile Percentile ] | * [http://en.wikipedia.org/wiki/Percentile Percentile ] | ||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 15:46, 8 August 2018
PERCENTILE (Array,kth)
- is the array of data .
- is the Percentile value.
- PERCENTILE(),returns the k-th percentile of values in a range.
Description
- This function gives the percentile value in a given range.
- Percentile means any of the 100 equal parts into which the range of the values of a set of data can be divided in order to show the distribution of those values.
- The percentile of a given value is determined by the percentage of the values that are smaller than that value.
- For example we can have the percentile is the value below which 25 percent of the observations may be found.
- The 25th percentile is called as the first quartile (Q1), the 50th percentile as the median quartile (Q2), and the 75th percentile as the third quartile (Q3).
- In general, percentiles and quartiles are specific types of quantiles.
- In , is the array of data that indicating relative standing and is the Percentile value in the range (inclusive).
- This function will return the result as error when
1. The array value is empty. 2. is non-numeric or or .
Examples
1.
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 5 | 7 | 2 | 9 |
=PERCENTILE(A1:D1,0.4) = 5.4
2.
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | 15 | 20 | 12 | 41 | 35 |
=PERCENTILE(A1:E1,0.721) = 33.26
3.
| A | B | C | |
|---|---|---|---|
| 1 | 2 | 3 | 4 |
=PERCENTILE(A1:A3,1.1) = NAN
Related Videos
See Also
References
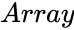 is the array of data .
is the array of data .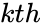 is the Percentile value.
is the Percentile value.
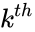 percentile value in a given range.
percentile value in a given range.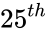 percentile is the value below which 25 percent of the observations may be found.
percentile is the value below which 25 percent of the observations may be found.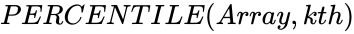 ,
,  (inclusive).
(inclusive).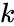 is non-numeric or
is non-numeric or 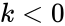 or
or 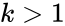 .
.