Difference between revisions of "Manuals/calci/PERCENTRANK"
Jump to navigation
Jump to search
| (14 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''PERCENTRANK( | + | <div style="font-size:30px">'''PERCENTRANK (Array,Number,Significance) '''</div><br/> |
| − | *<math> | + | *<math>Array</math> is the set of data and <math> Number</math> is the value to find the rank. |
| − | + | **PERCENTRANK(),returns the percentage rank of a value in a data set. | |
==Description== | ==Description== | ||
| Line 8: | Line 8: | ||
*For example, a test score that is greater than or equal to 50% of the scores of people taking the test is said to be at the 50th percentile rank. | *For example, a test score that is greater than or equal to 50% of the scores of people taking the test is said to be at the 50th percentile rank. | ||
*Percentile ranks are commonly used to clarify the interpretation of scores on standardized tests. | *Percentile ranks are commonly used to clarify the interpretation of scores on standardized tests. | ||
| − | * To find the percentile rank of a score is :<math>PR \%= \frac {L+( 0.5*S )}{N} | + | * To find the percentile rank of a score is :<math>PR \%= \frac {L+( 0.5*S )}{N}</math> |
Where, | Where, | ||
| − | L = Number of below rank, | + | <math>L</math> = Number of below rank, |
| − | S = Number of same rank, | + | <math>S</math> = Number of same rank, |
| − | N = Total numbers. | + | <math>N</math> = Total numbers. |
| − | *In PERCENTRANK( | + | *In <math>PERCENTRANK (Array,Number,Significance)</math>, <math>Array</math> is the array of numeric values and <math>Number</math> is the value to find the rank. |
| + | *This function gives the result as error when array is empty . | ||
| − | + | ==Examples== | |
| + | 1. | ||
| + | {| class="wikitable" | ||
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! !! A !! B !! C !! D !! E | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 3 || 4 || 1 || 2 ||1 | ||
| + | |} | ||
| + | =PERCENTRANK(A1:E1,2) = 0.5 | ||
| − | + | 2. | |
| − | + | {| class="wikitable" | |
| − | + | |+Spreadsheet | |
| − | + | |- | |
| − | + | ! !! A !! B !! C !! D !! E !! F | |
| − | + | |- | |
| − | + | ! 1 | |
| − | + | | 7 || 6 || 2 || 5 || 9 ||1 | |
| − | + | |} | |
| − | + | =PERCENTRANK(A1:F1,3) = 0.267 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | PERCENTRANK | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==Related Videos== | |
| − | + | {{#ev:youtube|aW2UZjoeljE|280|center|PERCENTRANK}} | |
| − | + | ==See Also== | |
| + | *[[Manuals/calci/MAX | MAX ]] | ||
| + | *[[Manuals/calci/MIN | MIN ]] | ||
| + | *[[Manuals/calci/MEDIAN | MEDIAN ]] | ||
| + | *[[Manuals/calci/QUARTILE | QUARTILE ]] | ||
| + | *[[Manuals/calci/PERCENTILE | PERCENTILE ]] | ||
| − | + | ==References== | |
| + | [http://en.wikipedia.org/wiki/Percentile_rank Percentile Rank ] | ||
| − | |||
| − | |||
| − | + | *[[Z_API_Functions | List of Main Z Functions]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *[[ Z3 | Z3 home ]] | |
| − | |||
Latest revision as of 15:56, 8 August 2018
PERCENTRANK (Array,Number,Significance)
- is the set of data and is the value to find the rank.
- PERCENTRANK(),returns the percentage rank of a value in a data set.
Description
- This function gives the percentage rank of a value in a given set of numbers.
- To calculate the relative standing of a data set we can use this function.
- For example, a test score that is greater than or equal to 50% of the scores of people taking the test is said to be at the 50th percentile rank.
- Percentile ranks are commonly used to clarify the interpretation of scores on standardized tests.
- To find the percentile rank of a score is :
Where, = Number of below rank, = Number of same rank, = Total numbers.
- In , is the array of numeric values and is the value to find the rank.
- This function gives the result as error when array is empty .
Examples
1.
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | 3 | 4 | 1 | 2 | 1 |
=PERCENTRANK(A1:E1,2) = 0.5
2.
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | 7 | 6 | 2 | 5 | 9 | 1 |
=PERCENTRANK(A1:F1,3) = 0.267
Related Videos
See Also
References
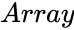 is the set of data and
is the set of data and 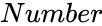 is the value to find the rank.
is the value to find the rank.
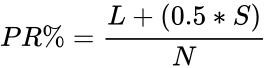
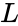 = Number of below rank,
= Number of below rank,
 = Number of same rank,
= Number of same rank,
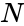 = Total numbers.
= Total numbers.
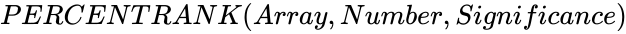 ,
,