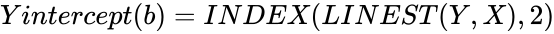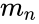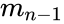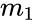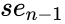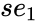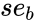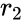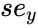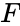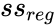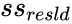Difference between revisions of "Manuals/calci/LINEST"
Jump to navigation
Jump to search
| (12 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | =LINEST( | + | <div style="font-size:30px">'''LINEST (YRange,XRanges,Constant,Stats)'''</div><br/> |
| − | |||
where, | where, | ||
| − | *<math> | + | *<math>YRange</math> is a set of Y values, |
| − | *<math> | + | *<math>XRanges</math> is an optional set of X values, |
| − | *<math> | + | *<math>Constant</math> is a logical value TRUE or FALSE, that decides whether to force the constant 'b' to 0, |
| − | *<math> | + | *<math>Stats</math> is a logical value TRUE or FALSE, that decides whether to return additional regression statistics. |
| − | + | **LINEST(), returns the parameters of a linear trend. | |
| − | LINEST() | ||
== Description == | == Description == | ||
| + | *This function is an array function that calculates the statistics for a line by using the 'least squares' method to calculate a straight line that closely fits the input data. | ||
*If 'Y' is the point on y-axis, 'X' is the point on x-axis, 'm' is a constant indicating slope of the line and 'b' is the constant value at which the line crosses y-axis (Y intercept), | *If 'Y' is the point on y-axis, 'X' is the point on x-axis, 'm' is a constant indicating slope of the line and 'b' is the constant value at which the line crosses y-axis (Y intercept), | ||
| − | + | then equation of line is - | |
| − | <math>Y=mX + b</math> | + | <math>Y=mX + b</math> |
*For multiple ranges of X-values, | *For multiple ranges of X-values, | ||
| − | <math>Y = m1X1 + m2X2 +......+ b</math> | + | <math>Y = m1X1 + m2X2 +......+ b</math> |
| − | *<math> | + | *Argument values <math>XRanges</math> and <math>YRange</math> should be numeric, else Calci displays NaN error message. |
| − | *If <math> | + | *The length of array of X values should be equal to length of array of Y values, else Calci displays #NULL error message. |
| − | *<math> | + | *<math>Constant</math> is a logical value that decides whether to make constant 'b' equal to 0. |
| − | *If <math> | + | *If <math>Constant</math> = TRUE or omitted, 'b' is calculated normally. If <math>Constant</math> = FALSE, 'b' is made equal to 0. |
| + | *<math>Stats</math> is a logical value that decides whether to display additional regression statistics. | ||
| + | *If <math>Stats</math> = TRUE, calci returns additional regression statistics. If <math>,Stats</math> = FALSE or omitted, Calci returns the values of 'm'(slope) and the constant 'b'. | ||
*When there is only one independent X variable, Slope(m) and Y intercept (b) can be calculated using following formulas - | *When there is only one independent X variable, Slope(m) and Y intercept (b) can be calculated using following formulas - | ||
| − | <math>Slope (m) = INDEX(LINEST(Y, X),1) </math> | + | <math>Slope (m) = INDEX(LINEST(Y, X),1) </math> |
| + | |||
| + | <math>Y intercept (b) = INDEX(LINEST(Y, X),2) </math> | ||
| + | *The additional regression is displayed in the following format where each statistic value is described as below- | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | <math>m_n</math> || <math>m_{n-1}</math> || --- || <math>m_1</math> || <math>b</math> | ||
| + | |- | ||
| + | | <math>se_n</math> || <math>se_{n-1}</math> || --- || <math>se_1</math> || <math>se_b</math> | ||
| + | |- | ||
| + | | <math>r_2</math> || <math>se_y</math> || || || | ||
| + | |- | ||
| + | | <math>F</math> || <math>d_f</math> || || || | ||
| + | |- | ||
| + | | <math>ss_{reg}</math> || <math>ss_{resld}</math> || || || | ||
| + | |} | ||
| − | <math>Y | + | *<math>m_n</math> is an array of constant multipliers for straight line equation |
| + | *<math>b</math> is the constant value of Y when X=0 | ||
| + | *<math>se_1</math> is the standard error value for m1 | ||
| + | *<math>se_b</math> is the standard error value for constant b | ||
| + | *<math>r_2</math> is the coefficient of determination | ||
| + | *<math>se_y</math> is the standard error value for Y estimate | ||
| + | *<math>F</math> is the observed F value | ||
| + | *<math>d_f</math> is the number of degrees of freedom | ||
| + | *<math>ss_{reg}</math> is the regression sum of squares | ||
| + | *<math>ss_{resld}</math> is the residual sum of squares | ||
== Examples == | == Examples == | ||
| Line 64: | Line 90: | ||
| class="sshl_f" | 10 | | class="sshl_f" | 10 | ||
| class="sshl_f" | | | class="sshl_f" | | ||
| − | + | ||
|} | |} | ||
| − | =LINEST(A2:A6,B2:B6,TRUE,FALSE) | + | =LINEST(A2:A6,B2:B6,TRUE,FALSE) : Calculates the statistics of line with Y co-ordinates in cells <br /> A2 to A6 and X co-ordinates in cells B2 to B6. Returns '''m=0''' and '''b=3''' as a result. |
| − | =LINEST(A2:A6,B2:B6,FALSE,FALSE) : Calculates the statistics of line with Y co-ordinates in | + | =LINEST(A2:A6,B2:B6,FALSE,FALSE): Calculates the statistics of line with Y co-ordinates in cells <br /> A2 to A6 and X co-ordinates in cells range B2 to B6. Returns '''m=0.4090909090909091''' and '''b=0''' as a result. |
| − | =LINEST(A2:A6,B2:B6,FALSE,TRUE) | + | |
| + | =LINEST(A2:A6,B2:B6,FALSE,TRUE) : Displays the additional regression statistics of line <br />with Y co-ordinates in cells A2 to A6 and X co-ordinates in cells B2 to B6 as shown below: | ||
<div id="5SpaceContent" class="zcontent" align="left"> | <div id="5SpaceContent" class="zcontent" align="left"> | ||
| Line 91: | Line 118: | ||
|} | |} | ||
| − | + | ||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|6wbcPbYbq6M|280|center|LINEST}} | ||
| + | |||
== See Also == | == See Also == | ||
| Line 98: | Line 129: | ||
== References == | == References == | ||
*[http://en.wikipedia.org/wiki/Linear_equation Linear Equation] | *[http://en.wikipedia.org/wiki/Linear_equation Linear Equation] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 16:13, 10 August 2018
LINEST (YRange,XRanges,Constant,Stats)
where,
- is a set of Y values,
- is an optional set of X values,
- is a logical value TRUE or FALSE, that decides whether to force the constant 'b' to 0,
- is a logical value TRUE or FALSE, that decides whether to return additional regression statistics.
- LINEST(), returns the parameters of a linear trend.
Description
- This function is an array function that calculates the statistics for a line by using the 'least squares' method to calculate a straight line that closely fits the input data.
- If 'Y' is the point on y-axis, 'X' is the point on x-axis, 'm' is a constant indicating slope of the line and 'b' is the constant value at which the line crosses y-axis (Y intercept),
then equation of line is -
- For multiple ranges of X-values,
- Argument values and should be numeric, else Calci displays NaN error message.
- The length of array of X values should be equal to length of array of Y values, else Calci displays #NULL error message.
- is a logical value that decides whether to make constant 'b' equal to 0.
- If = TRUE or omitted, 'b' is calculated normally. If = FALSE, 'b' is made equal to 0.
- is a logical value that decides whether to display additional regression statistics.
- If = TRUE, calci returns additional regression statistics. If = FALSE or omitted, Calci returns the values of 'm'(slope) and the constant 'b'.
- When there is only one independent X variable, Slope(m) and Y intercept (b) can be calculated using following formulas -
- The additional regression is displayed in the following format where each statistic value is described as below-
| --- | ||||
| --- | ||||
- is an array of constant multipliers for straight line equation
- is the constant value of Y when X=0
- is the standard error value for m1
- is the standard error value for constant b
- is the coefficient of determination
- is the standard error value for Y estimate
- is the observed F value
- is the number of degrees of freedom
- is the regression sum of squares
- is the residual sum of squares
Examples
| Y co-ordinates | X co-ordinates | |
| 1 | 2 | |
| 5 | 4 | |
| 4 | 6 | |
| 3 | 8 | |
| 2 | 10 |
=LINEST(A2:A6,B2:B6,TRUE,FALSE) : Calculates the statistics of line with Y co-ordinates in cells
A2 to A6 and X co-ordinates in cells B2 to B6. Returns m=0 and b=3 as a result. =LINEST(A2:A6,B2:B6,FALSE,FALSE): Calculates the statistics of line with Y co-ordinates in cells
A2 to A6 and X co-ordinates in cells range B2 to B6. Returns m=0.4090909090909091 and b=0 as a result. =LINEST(A2:A6,B2:B6,FALSE,TRUE) : Displays the additional regression statistics of line
with Y co-ordinates in cells A2 to A6 and X co-ordinates in cells B2 to B6 as shown below:
| 0.40909090909090906 | 0 |
| 0.14373989364401724 | |
| 0.6694214876033057 | 2.1320071635561044 |
| 8.099999999999998 | 4 |
| 36.81818181818181 | 18.181818181818183 |
Related Videos
See Also
References
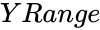 is a set of Y values,
is a set of Y values,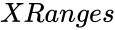 is an optional set of X values,
is an optional set of X values,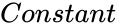 is a logical value TRUE or FALSE, that decides whether to force the constant 'b' to 0,
is a logical value TRUE or FALSE, that decides whether to force the constant 'b' to 0,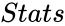 is a logical value TRUE or FALSE, that decides whether to return additional regression statistics.
is a logical value TRUE or FALSE, that decides whether to return additional regression statistics.
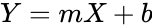
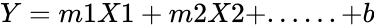
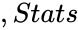 = FALSE or omitted, Calci returns the values of 'm'(slope) and the constant 'b'.
= FALSE or omitted, Calci returns the values of 'm'(slope) and the constant 'b'.