Difference between revisions of "Manuals/calci/FOURIERANALYSIS"
Jump to navigation
Jump to search
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''FOURIERANALYSIS( | + | <div style="font-size:30px">'''FOURIERANALYSIS (Array,NewTableFlag)'''</div><br/> |
| − | *<math> | + | *<math>Array</math> is the set of numbers. |
| + | *<math>NewTableFlag</math> is the value true or false. | ||
| + | **FOURIERANALYSIS() is a method of dissociating time series or spatial data into sets of sine and cosine waves | ||
==Description== | ==Description== | ||
| Line 7: | Line 9: | ||
*It converts a set of numbers into another equal sized set of numbers. | *It converts a set of numbers into another equal sized set of numbers. | ||
*It is the process of analyzing a complex wave by separating it into a plurality of component wave, each of a particular frequency, amplitude and phase displacement. | *It is the process of analyzing a complex wave by separating it into a plurality of component wave, each of a particular frequency, amplitude and phase displacement. | ||
| − | *In <math>FOURIERANALYSIS( | + | *In <math>FOURIERANALYSIS (Array,NewTableFlag)</math>, <math>Array</math>is the set of real numbers. |
| − | *But the size of the set to be a power of 2.i.e., | + | *But the size of the set to be a power of 2.i.e., Array is the size of the numbers can be 2,4,8,16.... |
*So we can form the Fourier transform of a set of 64 numbers, but not a set of 50 numbers. | *So we can form the Fourier transform of a set of 64 numbers, but not a set of 50 numbers. | ||
*In the discrete Fourier Transform (DFT) decomposes the input time series into a set of cosine functions. | *In the discrete Fourier Transform (DFT) decomposes the input time series into a set of cosine functions. | ||
Latest revision as of 16:22, 17 August 2018
FOURIERANALYSIS (Array,NewTableFlag)
- is the set of numbers.
- is the value true or false.
- FOURIERANALYSIS() is a method of dissociating time series or spatial data into sets of sine and cosine waves
Description
- This function gives the value of the discrete fourier tranform.
- Fourier analysis is the study of the way general functions may be represented by sums of simpler trigonometric functions.
- It converts a set of numbers into another equal sized set of numbers.
- It is the process of analyzing a complex wave by separating it into a plurality of component wave, each of a particular frequency, amplitude and phase displacement.
- In , is the set of real numbers.
- But the size of the set to be a power of 2.i.e., Array is the size of the numbers can be 2,4,8,16....
- So we can form the Fourier transform of a set of 64 numbers, but not a set of 50 numbers.
- In the discrete Fourier Transform (DFT) decomposes the input time series into a set of cosine functions.
- It is having the following properties
1.The transformed data is no longer in the time domain. 2. The transformation operates on the whole data set. It is not a point-by-point transformation. 3.The transformed data is complex (not real-valued).
- So the output of this function is Hermite symmetric, which means that the positive and negative real parts will be identical, and that the positive and negative imaginary parts will be the same, but of opposite sign.
- The formula for the DFT is :
where is the amplitude, is the phase value in radians.
- is the fundamental or principal radian frequency and , is the number of observations in the equally-spaced input time series. is the is the number of pairs.
- This function will give the result as error when
1. any one of the argument is nonnumeric. 2. The number of input value is not a power of 2.
Examples
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| 1 | 21 | 28 | 34 | 46 | 15 | 10 | 4 | 9 |
| 2 | 6 | 17 | 22 | 16 | 39 | 50 | 11 | -27 |
- =FOURIERANALYSIS(A1:D1)
| Input | Output |
|---|---|
| 21 | 129+0i |
| 28 | -13.000000000000002+18i |
| 34 | -19+0i |
| 46 | -12.999999999999998 -18i |
- =FOURIERANALYSIS(A2:H2)
| Input | Output |
|---|---|
| 6 | 134+0i |
| 17 | -86.7401153701776 -18.07106781186548i |
| 22 | 12.000000000000005 -78i |
| 16 | 20.740115370177605+3.928932188134528i |
| 39 | 22+0i |
| 50 | 20.740115370177605 -3.928932188134521i |
| 11 | 11.999999999999995+78i |
| -27 | -86.7401153701776+18.071067811865472i |
Related Videos
See Also
References
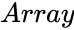 is the set of numbers.
is the set of numbers.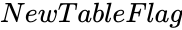 is the value true or false.
is the value true or false.
 ,
, 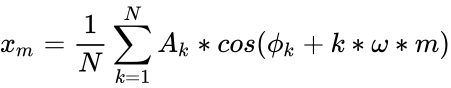 where
where 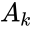 is the amplitude,
is the amplitude,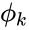 is the phase value in radians.
is the phase value in radians.
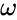 is the fundamental or principal radian frequency and
is the fundamental or principal radian frequency and 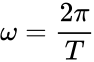 ,
, 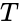 is the number of observations in the equally-spaced input time series.
is the number of observations in the equally-spaced input time series.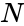 is the is the number of pairs.
is the is the number of pairs.