Difference between revisions of "Manuals/calci/GOLDENRATIO"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> '''GOLDENRATIO'''(phismall) where '''phismall''' is true or false </div> ---- <div id="1SpaceContent" cl...") |
|||
| (10 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''GOLDENRATIO(phiSmall)'''</div><br/> |
| + | *where <math>phiSmall</math> is the logical value TRUE or FALSE. | ||
| + | **GOLDENRATIO() returns the ratio of the longer part divided by the smaller part is also equal to the whole length divided by the longer part. | ||
| − | + | == Description == | |
| − | + | *Two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. | |
| + | *Golden ratio is represented as '''φ(phi or Smallphi)''' and its conjugate is represented as '''Φ(Phi or capitalphi)'''. | ||
| + | *If 'a' and 'b' are two quantities with 'a>b', then | ||
| − | + | φ = <math>\frac{(a + b)}{a}</math> = <math>\frac {a}{b}</math> | |
| + | *Using quadratic formula, golden ratio is represented as - | ||
| − | </ | + | <math>\phi</math> = <math>\frac{(1 + \sqrt 5)}{2}</math> = 1.618033988749895 |
| − | |||
| − | < | ||
| − | + | <math>\Phi</math> = <math>\frac{(1 - \sqrt 5)}{2}</math> = -0.6180339887498948 (Absolute value 0.6180339887498948 is considered as capitalphi) | |
| − | </ | + | *Argument <math>phismall</math> can be logical values TRUE (or 1) or FALSE (or 0). Any other argument values are ignored and Calci assumes it to be TRUE or 1. |
| − | + | *If argument <math>phismall</math> is omitted, Calci assumes it as TRUE or 1 and displays the output as ''0.6180339887498948''. | |
| − | < | + | *If argument is invalid, Calci returns a #NULL error message. |
| − | + | == Examples == | |
| − | + | GOLDENRATIO(TRUE) ''returns 0.6180339887498948'', value of capitalphi Φ | |
| − | |||
| − | |||
| − | GOLDENRATIO | + | GOLDENRATIO(1) ''returns 0.6180339887498948'', value of capitalphi Φ |
| − | + | GOLDENRATIO(FALSE) ''returns 1.618033988749895'', value of smallphi φ | |
| − | |||
| − | |||
| − | + | GOLDENRATIO() ''returns 0.6180339887498948'', value of capitalphi Φ | |
| − | + | ==Related Videos== | |
| − | + | {{#ev:youtube|5zosU6XTgSY|280|center|GOLDENRATIO}} | |
| − | + | == See Also == | |
| − | + | *[[Manuals/calci/GOLDENANGLE | GOLDENANGLE]] | |
| − | + | == References == | |
| − | + | *[http://en.wikipedia.org/wiki/Golden_ratio Golden Ratio] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | + | *[[Z_API_Functions | List of Main Z Functions]] | |
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 16:25, 17 August 2018
GOLDENRATIO(phiSmall)
- where is the logical value TRUE or FALSE.
- GOLDENRATIO() returns the ratio of the longer part divided by the smaller part is also equal to the whole length divided by the longer part.
Description
- Two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities.
- Golden ratio is represented as φ(phi or Smallphi) and its conjugate is represented as Φ(Phi or capitalphi).
- If 'a' and 'b' are two quantities with 'a>b', then
φ = =
- Using quadratic formula, golden ratio is represented as -
= = 1.618033988749895
= = -0.6180339887498948 (Absolute value 0.6180339887498948 is considered as capitalphi)
- Argument can be logical values TRUE (or 1) or FALSE (or 0). Any other argument values are ignored and Calci assumes it to be TRUE or 1.
- If argument is omitted, Calci assumes it as TRUE or 1 and displays the output as 0.6180339887498948.
- If argument is invalid, Calci returns a #NULL error message.
Examples
GOLDENRATIO(TRUE) returns 0.6180339887498948, value of capitalphi Φ
GOLDENRATIO(1) returns 0.6180339887498948, value of capitalphi Φ
GOLDENRATIO(FALSE) returns 1.618033988749895, value of smallphi φ
GOLDENRATIO() returns 0.6180339887498948, value of capitalphi Φ
Related Videos
See Also
References
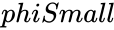 is the logical value TRUE or FALSE.
is the logical value TRUE or FALSE.
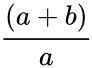 =
= 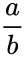
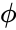 =
=  = 1.618033988749895
= 1.618033988749895
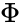 =
=  = -0.6180339887498948 (Absolute value 0.6180339887498948 is considered as capitalphi)
= -0.6180339887498948 (Absolute value 0.6180339887498948 is considered as capitalphi)
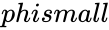 can be logical values TRUE (or 1) or FALSE (or 0). Any other argument values are ignored and Calci assumes it to be TRUE or 1.
can be logical values TRUE (or 1) or FALSE (or 0). Any other argument values are ignored and Calci assumes it to be TRUE or 1.