Difference between revisions of "Manuals/calci/ACKERMANN"
Jump to navigation
Jump to search
| Line 20: | Line 20: | ||
| − | + | ==See Also== | |
*[[Z_API_Functions | List of Main Z Functions]] | *[[Z_API_Functions | List of Main Z Functions]] | ||
*[[ Z3 | Z3 home ]] | *[[ Z3 | Z3 home ]] | ||
Revision as of 16:05, 21 August 2018
ACKERMANN(m,n)
- and are the positive integers.
Description
- The Ackermann function is a classic example of a recursive function, notable especially because it is not a primitive recursive function.
- All primitive recursive functions are total and computable, but the Ackermann function illustrates that not all total computable functions are primitive recursive.
- Its arguments are never negative and it always terminates.
- The two-argument Ackermann–Péter function, is defined as follows:
\\
for nonnegative integers m and n.
- Its value grows rapidly, even for small inputs.
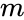 and
and  are the positive integers.
are the positive integers.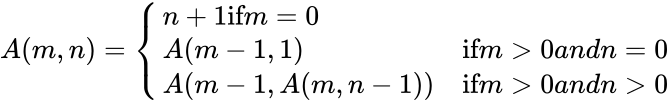 \\
\\